题目内容
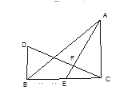
【题目】已知:如图,△ABC中,AB=AC,D是BC上一点,点E、F分别在AB、AC上,BD=CF,CD=BE,G为EF的中点.

求证:(1)△BDE≌△CFD(2)DG⊥EF.
【答案】(1)见详解;(2)见详解.
【解析】
(1)由在△ABC中,AB=AC,可知∠B=∠C,又知三角形两边相等,故由SAS判定△BDE≌△CFD,
(2)由(1)问两三角形全等,可证DE=DF,又知G为EF的中点,故能证DG⊥EF.
解:(1)在△ABC中,AB=AC,
∴∠B=∠C,
∵BD=CF,CD=BE,
∴△BDE≌△CFD;
(2)由(1)知△BDE≌△CFD,
∴DE=DF,即△DEF是等腰三角形,
∵G为EF的中点,
由等腰三角形三线合一定理,则
∴DG⊥EF.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目