题目内容
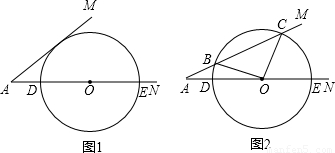
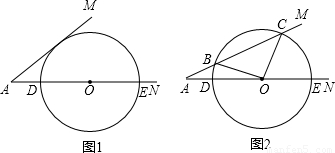
已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,设AD为x.
(1)如图1,当x为何值时,⊙O与AM相切;
(2)如图2,当x为何值时,⊙O与AM相交于B、C两点,且∠BOC=90度.
(1)如图1,当x为何值时,⊙O与AM相切;
(2)如图2,当x为何值时,⊙O与AM相交于B、C两点,且∠BOC=90度.
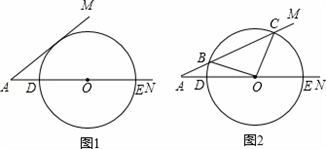
解:(1)如图1,过O作OF⊥AM于F, 当OF=r=2时,⊙O与AM相切,
此时OA=OF÷sin30°=4,故x=AD=2;
(2)如图2,过O点作OG⊥AM于G当∠BOC=90°,
∵OB=OC=2,
∴BC=2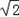
∵OG⊥BC,
∴BG=CG=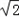 ,
,
∴OG=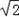 ,
,
又∵∠A=30°,
∴OA=2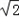 ,
,
∴x=AD=(2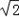 ﹣2).
﹣2).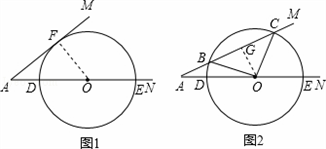

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
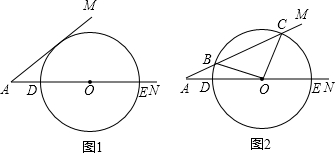
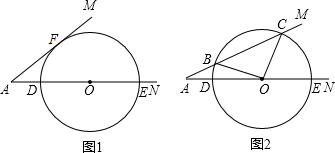
 如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?
如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?