题目内容
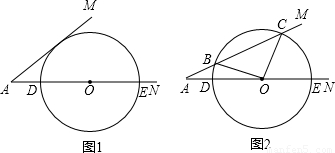
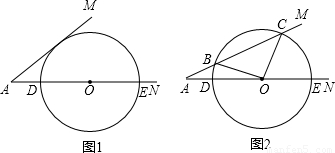
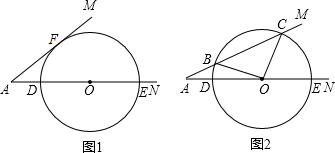
已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,设AD为x.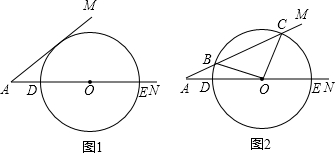
(1)如图1,当x为何值时,⊙O与AM相切;
(2)如图2,当x为何值时,⊙O与AM相交于B、C两点,且∠BOC=90°.
分析:(1)过O作OF⊥AM于F,根据切线的概念,切线到圆心的距离等于半径故当OF=r=2时,⊙O与AM相切,然后解直角三角形求得AD的值;
(2)过O点作OG⊥AM于G,证得△OBC,△BGO与△CGO是等腰直角三角形,再解直角三角形,求得AD的值.
(2)过O点作OG⊥AM于G,证得△OBC,△BGO与△CGO是等腰直角三角形,再解直角三角形,求得AD的值.
解答: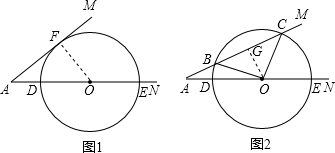 解:(1)如图1,过O作OF⊥AM于F,
解:(1)如图1,过O作OF⊥AM于F,
当OF=r=2时,⊙O与AM相切,
此时OA=OF÷sin30°=4,
故x=AD=2;
(2)如图2,过O点作OG⊥AM于G
当∠BOC=90°,
∵OB=OC=2,
∴BC=2
又∵OG⊥BC,
∴BG=CG=
,
∴OG=
BC=
,
又∵∠A=30°,
∴OA=2
,
∴x=AD=2
-2.
 解:(1)如图1,过O作OF⊥AM于F,
解:(1)如图1,过O作OF⊥AM于F,当OF=r=2时,⊙O与AM相切,
此时OA=OF÷sin30°=4,
故x=AD=2;
(2)如图2,过O点作OG⊥AM于G
当∠BOC=90°,
∵OB=OC=2,
∴BC=2
| 2 |
又∵OG⊥BC,
∴BG=CG=
| 2 |
∴OG=
| 1 |
| 2 |
| 2 |
又∵∠A=30°,
∴OA=2
| 2 |
∴x=AD=2
| 2 |
点评:本题利用了切线的概念,等腰直角三角形的判定和性质,垂径定理,正弦的定义等知识求解.

练习册系列答案
相关题目
 如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?
如图,已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x,问:当x为何值时,⊙O与AM相切?