ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊХзЮяЯп
жаЃЌвбжЊХзЮяЯп![]() гыжБЯп
гыжБЯп![]() ЖМОЙ§
ЖМОЙ§![]() ЁЂ
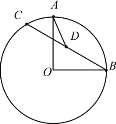
ЁЂ![]() СНЕуЃЌИУХзЮяЯпЕФЖЅЕуЮЊCЃЎ
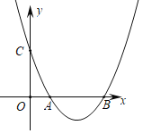
СНЕуЃЌИУХзЮяЯпЕФЖЅЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпКЭжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
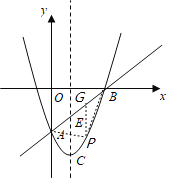
ЃЈ2ЃЉЩшжБЯп![]() гыИУХзЮяЯпЕФЖдГЦжсНЛгкЕуEЃЌдкЩфЯп
гыИУХзЮяЯпЕФЖдГЦжсНЛгкЕуEЃЌдкЩфЯп![]() ЩЯЪЧЗёДцдквЛЕуMЃЌЙ§MзїxжсЕФДЙЯпНЛХзЮяЯпгкЕуNЃЌЪЙЕуMЁЂNЁЂCЁЂEЪЧЦНааЫФБпаЮЕФЫФИіЖЅЕуЃПШєДцдкЃЌЧѓЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЩЯЪЧЗёДцдквЛЕуMЃЌЙ§MзїxжсЕФДЙЯпНЛХзЮяЯпгкЕуNЃЌЪЙЕуMЁЂNЁЂCЁЂEЪЧЦНааЫФБпаЮЕФЫФИіЖЅЕуЃПШєДцдкЃЌЧѓЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшЕуPЪЧжБЯп![]() ЯТЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЕБ
ЯТЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЕБ![]() УцЛ§зюДѓЪБЃЌЧѓЕуPЕФзјБъЃЌВЂЧѓ
УцЛ§зюДѓЪБЃЌЧѓЕуPЕФзјБъЃЌВЂЧѓ![]() УцЛ§ЕФзюДѓжЕЃЎ
УцЛ§ЕФзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌЃЈ2ЃЉ
ЃЌЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЎЃЈ3ЃЉЕБ
ЃЎЃЈ3ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() УцЛ§ЕФзюДѓжЕЪЧ
УцЛ§ЕФзюДѓжЕЪЧ![]() ЃЌДЫЪБPЕузјБъЮЊ
ЃЌДЫЪБPЕузјБъЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
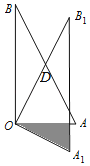
ЃЈ1ЃЉНЋ![]() ЁЂ
ЁЂ![]() СНЕузјБъЗжБ№ДњШыЖўДЮКЏЪ§ЕФНтЮіЪНКЭвЛДЮКЏЪ§НтЮіЪНМДПЩЧѓНтЃЛ
СНЕузјБъЗжБ№ДњШыЖўДЮКЏЪ§ЕФНтЮіЪНКЭвЛДЮКЏЪ§НтЮіЪНМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЯШЧѓГіCЕузјБъКЭEЕузјБъЃЌдђ![]() ЃЌЗжСНжжЧщПіЬжТлЃКЂйШєЕуMдкxжсЯТЗНЃЌЫФБпаЮ
ЃЌЗжСНжжЧщПіЬжТлЃКЂйШєЕуMдкxжсЯТЗНЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЌдђ
ЮЊЦНааЫФБпаЮЃЌдђ![]() ЃЌЂкШєЕуMдкxжсЩЯЗНЃЌЫФБпаЮ
ЃЌЂкШєЕуMдкxжсЩЯЗНЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЌдђ
ЮЊЦНааЫФБпаЮЃЌдђ![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌПЩЗжБ№ЕУЕНЗНГЬЧѓГіЕуMЕФзјБъЃЛ
ЃЌПЩЗжБ№ЕУЕНЗНГЬЧѓГіЕуMЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЃЌзї![]() жсНЛжБЯп
жсНЛжБЯп![]() гкЕуGЃЌЩш
гкЕуGЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌПЩгЩ
ЃЌПЩгЩ![]() ЃЌЕУЕНmЕФБэДяЪНЃЌРћгУЖўДЮКЏЪ§ЧѓзюжЕЮЪЬтХфЗНМДПЩЃЎ
ЃЌЕУЕНmЕФБэДяЪНЃЌРћгУЖўДЮКЏЪ§ЧѓзюжЕЮЪЬтХфЗНМДПЩЃЎ
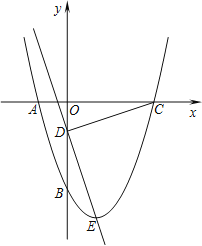
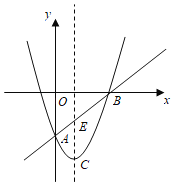
НтЃКЃЈ1ЃЉЁпХзЮяЯп![]() ОЙ§
ОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЃЌ
СНЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЁпжБЯп![]() ОЙ§
ОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЃЌ
СНЕуЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЃЈ2ЃЉЁп![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФЖЅЕуCЕФзјБъЮЊ![]() ЃЌ
ЃЌ
Ёп![]() жсЃЌ
жсЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
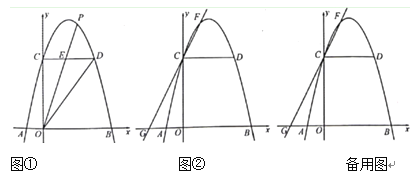
ЂйШчЭМЃЌШєЕуMдкxжсЯТЗНЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЌдђ
ЮЊЦНааЫФБпаЮЃЌдђ![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
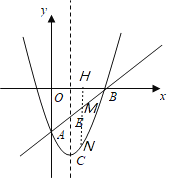
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
ЂкШчЭМЃЌШєЕуMдкxжсЩЯЗНЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЌдђ
ЮЊЦНааЫФБпаЮЃЌдђ![]() ЃЌ
ЃЌ

Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
злКЯПЩЕУMЕуЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМЃЌзї![]() жсНЛжБЯп
жсНЛжБЯп![]() гкЕуGЃЌ
гкЕуGЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() УцЛ§ЕФзюДѓжЕЪЧ
УцЛ§ЕФзюДѓжЕЪЧ![]() ЃЌДЫЪБPЕузјБъЮЊ
ЃЌДЫЪБPЕузјБъЮЊ![]() ЃЎ
ЃЎ

 ЖсЙкН№ОэШЋФмСЗПМЯЕСаД№АИ
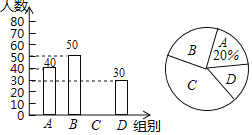
ЖсЙкН№ОэШЋФмСЗПМЯЕСаД№АИЁОЬтФПЁПдФЖСЖдбЇЩњЕФГЩГЄгазХЩюдЖЕФгАЯьЃЎФГжабЇЮЊСЫНтбЇЩњУПжмПЮгрдФЖСЕФЪБМфЃЌдкБОаЃЫцЛњГщШЁШєИЩУћбЇЩњНјааЕїВщЃЌВЂвРОнЕїВщНсЙћОжЦСЫвдЯТВЛЭъећЕФЭГМЦЭМБэЃЎ
зщБ№ | ЪБМфЃЈаЁЪБЃЉ | ЦЕЪ§ЃЈШЫЪ§ЃЉ | ЦЕТЪ |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
КЯМЦ | 1 |
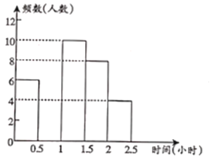
ЧыИљОнЭМБэжаЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБэжаЕФ![]() ЃЌ
ЃЌ![]() ЃЌНЋЦЕЪ§ЗжВМжБЗНЭМВЙШЋЃЛ
ЃЌНЋЦЕЪ§ЗжВМжБЗНЭМВЙШЋЃЛ
ЃЈ2ЃЉЙРМЦИУаЃ2000УћбЇЩњжаЃЌУПжмПЮгрдФЖСЪБМфВЛзу1аЁЪБЕФбЇЩњДѓдМгаЖрЩйУћЃП
ЃЈ3ЃЉ![]() зщЕФ4ШЫжаЃЌга1УћФаЩњКЭ3УћХЎЩњЃЌИУаЃМЦЛЎдк
зщЕФ4ШЫжаЃЌга1УћФаЩњКЭ3УћХЎЩњЃЌИУаЃМЦЛЎдк![]() зщбЇЩњжаЫцЛњбЁГіСНШЫЯђШЋаЃЭЌбЇзїЖСЪщаФЕУБЈИцЃЌЧѓГщШЁЕФСНУћбЇЩњИеКУЪЧ1УћФаЩњКЭ1УћХЎЩњЕФИХТЪЃЎ
зщбЇЩњжаЫцЛњбЁГіСНШЫЯђШЋаЃЭЌбЇзїЖСЪщаФЕУБЈИцЃЌЧѓГщШЁЕФСНУћбЇЩњИеКУЪЧ1УћФаЩњКЭ1УћХЎЩњЕФИХТЪЃЎ