题目内容
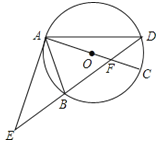
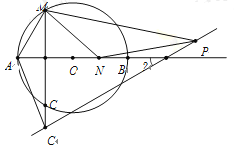
【题目】如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
(1)若AM=AC,点N与点O重合,则α= °;
(2)若点C、点N的位置如图所示,求α的度数;
(3)当直线PC与⊙O相切时,则MC的长为 .
【答案】(1)30(2)30°(3)![]()
【解析】
试题分析:(1)根据AM=AC,MC垂直平分AO,OM=OA,可求得△MAO的形状,然后根据点C在圆上,AP是圆O的直径,从而可以求得α的值;
(2)根据AM=AC,MC垂直平分AO,OM=OA,可求得△MAO的形状,△MNP∽△MAC,从而可以求得∠AMC和α的值;
(3)根据题意和图形,以及(2)中的α的值,直线PC与圆O相切,可以分别求得MD、DC的长,从而可以求得MC的长.
试题解析:(1)如图 ,α= 30 °;
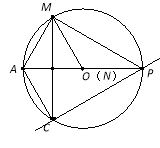
如图一所示:
∵AM=AC,MC垂直平分AO,OM=OA
∴MA=AC=MO=OA
∵点M在圆上
∴点C在圆上
∵AP是圆O的直径
∴∠ACP=90°
∵AP=2AC
∴∠APC=30°
即α=30°
(2)连接MO,

∵MC垂直平分AO,∴MA=MO=AO
∴∠AMO=60°,则∠AMC=30°
∵△MAQ∽△MNP,
∴![]() ,
,![]() ,
,
∴∠AMN=∠QMP,
∴△AMN∽△QMP,
∴∠MAN=∠MQP,
∴α=∠AMQ=30°;
(3)连接OE,如图三所示
∵AB=2,MC垂直平分AO
∴AO=1,DO=![]() ,MD=
,MD=![]()
由(2)可得α=30°
∵OE=1,∠OEF=90°
∴OF=2OE=2
∴DF=![]()
∴DC=DF·tanα=![]()
∴MC=MD+DC=![]()


练习册系列答案
相关题目