��Ŀ����
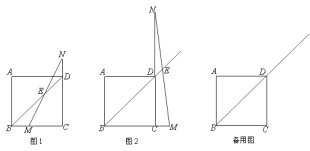
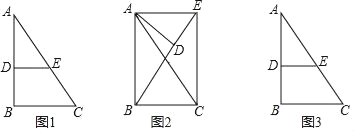
����Ŀ����1���۲췢�֣���ͼ1����Rt��ABC�У���B��90�㣬��D�ڱ�AB�ϣ���D��DE��BC��AC��E��AB��5��AD��3��AE��4����գ�
����ABC���ADE�Ƿ����ƣ���ֱ�ӻش��� ����
��AC���� ����DE���� ����
��2����չ̽��������ADE�ƶ���A��ת��ͼ2��ʾ��λ�ã������ADB���AEC�Ƿ����ƣ��������ƣ�˵�����ɣ������ƣ���֤����
��3��Ǩ��Ӧ�ã�����ADE�ƶ���A��ת����B��D��E��ͬһ��ֱ����ʱ��ֱ��д���߶�BE�ij���
���𰸡���1������������![]() ��
��![]() ����2����ADB�ס�AEC����3��4+
����2����ADB�ס�AEC����3��4+![]() ��4��
��4��![]() ��
��
��������
(1)�ٸ������������ε��ж��������
�ڸ��ݹ��ɶ������DE���������������ε������г�����ʽ�����AC��
(2)������ת�任�����ʵõ���BAD����CAE���������߶�Ӧ�ɱ������н���ȵ���������������֤����
(3)���ݹ��ɶ������BD��������������㼴�ɣ�
�⣺��1���١�DE��BC��
���ABC�ס�ADE��
�ʴ�Ϊ�����ƣ�
�ڡ�DE��BC��
���ADE����B��90�㣬
��DE��![]() ��
��![]() ��
��
�ߡ�ABC�ס�ADE��
��![]() ����
����![]() ��
��
��ã�AC��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��2����ADB�ס�AEC��
�������£�����ת�任�����ʿ�֪����BAD����CAE��
�ɣ�1���ã�![]() ���֡�BAD����CAE��
���֡�BAD����CAE��
���ADB�ס�AEC��
��3����ͼ2����Rt��ADB�У�BD��![]() ��4��
��4��
�ߵ�B��D��E��ͬһ��ֱ���ϣ�
��BE��BD+DE��4+![]() ��
��
��ͼ3��BE��BD��DE��4��![]() ��
��
��������������ADE�ƶ���A��ת����B��D��E��ͬһ��ֱ����ʱ���߶�BE�ij�Ϊ4+![]() ��4��
��4��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ����һ�������Ŀڴ���װ��ֻ����ɫ��ͬ�ĺڡ���������ɫ����20ֻ��ijѧϰС��������ʵ�飬������Ⱥ�����������һ���������ɫ���ٰ����Żش��У������ظ����±�ʾ������е�һ��ͳ�����ݣ�
����Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
��������Ĵ���m | 58 | 96 | 116 | 295 | 484 | 601 |
���������Ƶ�� | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
�����ڴ��а���Լ��(���� )ֻ��
A. 8 B. 9 C. 12 D. 13