题目内容
【题目】如图，已知梯形ABCD中，AD∥BC，∠C=90°，以CD为直径的圆与AB相切，AB=6，求梯形ABCD的中位线长．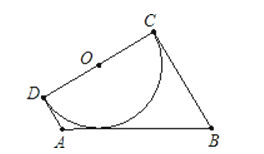
【答案】解：作OM⊥AB于M，连接OA、OB．
∵AD∥BC，∠C=90°，
∴∠D=180﹣∠C=90°，
∴以CD为直径的圆与AD、BC相切
∵以CD为直径的圆与AB相切，
∴AD=AM，BM=BC，
∴梯形ABCD的中位线长=
（AD+BC）=AB=3．
故梯形ABCD的中位线长为3．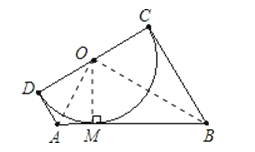
【解析】作OM⊥AB于M，连接OA、OB，证得AD=AM，BM=BC，用梯形的中位线定理求中位线长为3．
【考点精析】根据题目的已知条件，利用切线的性质定理的相关知识可以得到问题的答案，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．
练习册系列答案
相关题目
