Question

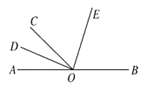
【题目】如图1，直线，的平分线交于点．

（1）求证：；

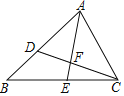
（2）如图2，过点作于点，交于点，探究与之间的数量关系，并证明你的猜想；

（3）如图3，在（2）的条件下，的平分线交延长线于点，为延长线上一点，，将延直线翻折，所得直线交于，交于，若，求的度数．

Answer 1

【答案】（1）证明见解析；（2）；（3）．

【解析】

（1）根据平行线的性质定理得到内错角相等,再根据角平分线的性质,即可得到等角.

（2）根据平行与垂直的性质,可得,而为的外角,根据三角形的外角定理即可解答.

（3）根据题目中已给的数量关系, 求的度数可转化为先求的度数,根据折叠的性质和平行线的性质,可将多个角的复杂数量关系转移到中,结果证明它是个等腰直角三角形,如此可解.

（1）证明: ,

,

又评分,

,

.

（2）为的外角,

,

又

,

即.

（3）如图,

根据折叠的性质,

,

,

,

,

,

,,

,

在中, ,

为等腰直角三角形, ,

,

,

.