题目内容
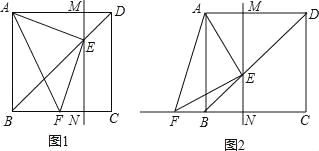
【题目】如图,点 E 是边长为 1 的正方形 ABCD 的对角线 BD 上的一个动点(不与 B、D 两点重合),过点 E 作直线 MN∥DC,交 AD 于 M,交 BC 于 N,连接 AE,作 EF⊥AE 于 E,交直线 CB 于 F.
(1)如图 1,当点 F 在线段 CB 上时,通过观察或测量,猜想△AEF 的形状,并证明你的猜想;
(2)如图 2,当点 F 在线段 CB 的延长线上时,其它条件不变,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由;
(3)在点 E 从点D 向点B 的运动过程中,四边形 AFNM 的面积是否会发生变化?若发生了变化,请说明理由;若没有发生变化,请求出其面积的值.
【答案】(1)△AEF是等腰直角三角形,证明见解析;(2)△AEF是等腰直角三角形,证明见解析;(3)四边形 AFNM 的面积没有发生改变,都是![]() .
.
【解析】
![]() 根据四边形 ABCD 是正方形,BD 是对角线,且 MN∥BA,求证△
根据四边形 ABCD 是正方形,BD 是对角线,且 MN∥BA,求证△
DEM 和△BNE 都是等腰直角三角形.又利用 EF⊥AE,可得∠EFN=∠AEM,然后即可求证,△AME≌△ENF;
![]() 利用(1)中证法求出 BN=EN=AM,∠AEM=∠EFN,即可得出答案;
利用(1)中证法求出 BN=EN=AM,∠AEM=∠EFN,即可得出答案;
![]() 分两种情况进行讨论:(i)当点 E 运动到 BD 的中点时,利用四边形 AFNM
分两种情况进行讨论:(i)当点 E 运动到 BD 的中点时,利用四边形 AFNM
是矩形,可得 S四边形AFNM=![]()
(ii)当点 E 不在 BD 的中点时,点 E 在运动(与点 B、D 不重合)的过程中,四边形 AFNM 是直角梯形.由(1)知,△AME≌△ENF,同理,图(2)△AME≌△ENF,然后即可得出结论.
(1)∵四边形 ABCD 是正方形,BD 是对角线,且 MN∥AB,
∴四边形 ABNM 和四边形 MNCD 都是矩形,
△NEB 和△MDE 都是等腰直角三角形.
∴∠AEF=∠ENF=90°,MN=BC=AB,EN=BN
![]()
即 EN=AM,
又∵∠AEM+∠FEN=90°,∠AEM+∠EAM=90°
∴∠EAM=∠FEN,
∵∠AME=∠ENF=90°,
∴△AME≌△ENF(ASA);
∴AE=BE,
∵AE⊥EF,
∴△AEF 是等腰直角三角形;
(2)由(1)同理可得:
∴BN=EN=AM,
∠AEM=∠EFN,
∵∠AME=∠ENF=90°
∴△AME≌△ENF(ASA);
∴AE=EF,
∵AE⊥EF,
∴△AEF 是等腰直角三角形;
四边形 AFNM 的面积没有发生变化
(i)当点 E 运动到 BD 的中点时,
四边形 AFNM 是矩形,S 四边形AFNM=![]()
(ii)当点 E 不在 BD 的中点时,点 E 在运动(与点 B、D 不重合)的过程中,四边形 AFNM 是直角梯形.
由(1)知,△AME≌△ENF,
同理,图(2),△AME≌△ENF,
∴FN=EM=DM.
∴FN+AM=DM+AM=AD=1
这时,S 四边形AFNM![]()
综合(i)、(ii)可知四边形 AFNM 的面积没有发生改变,都是![]() .
.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案