题目内容
【题目】定义:把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.
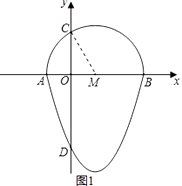
如图,抛物线y=x2﹣2x﹣3与x轴交于点A,B,与y轴交于点D,以AB为直径,在x轴上方作半圆交y轴于点C,半圆的圆心记为M,此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”.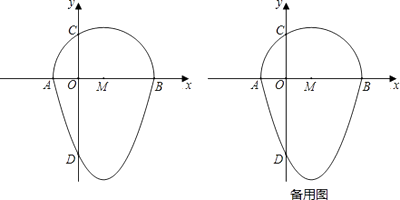
(1)直接写出点A,B,C的坐标及“蛋圆”弦CD的长;
A , B , C , CD=;
(2)如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
①求经过点C的“蛋圆”切线的解析式;
②求经过点D的“蛋圆”切线的解析式;
(3)由(2)求得过点D的“蛋圆”切线与x轴交点记为E,点F是“蛋圆”上一动点,试问是否存在S△CDE=S△CDF , 若存在请求出点F的坐标;若不存在,请说明理由;
(4)点P是“蛋圆”外一点,且满足∠BPC=60°,当BP最大时,请直接写出点P的坐标.
【答案】
(1)(﹣1,0);(3,0);(0, ![]() );3+
);3+ ![]()
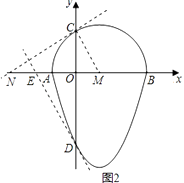
(2)解:①如图2,NC⊥CM,可求得N(﹣3,0),
∴经过点C的“蛋圆”切线的解析式为: ![]() ,
,
②过点D的“蛋圆”切线的解析式为:y=kx﹣3,
由 ![]() ,
,
得:x2﹣(2+k)x=0,
∵直线与抛物线只有一个交点,
∴k=﹣2,
∴经过点D的“蛋圆”切线的解析式为:y=﹣2x﹣3
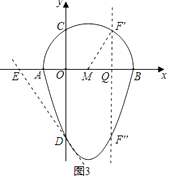
(3)解:如图3,∵经过点D的“蛋圆”切线的解析式为:y=﹣2x﹣3,
∴E点坐标为( ![]() ,0),
,0),
∵S△CDE=S△CDF,
∴F点的横坐标为 ![]() ,
,
在Rt△MQF1中可求得F′Q= ![]() ,
,
把x= ![]() 代入y=x2﹣2x﹣3,可求得y=
代入y=x2﹣2x﹣3,可求得y= ![]() .
.
∴F′( ![]() ,
, ![]() ),F′′(
),F′′( ![]() ,
, ![]() )
)
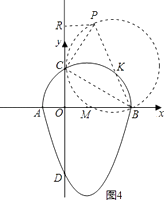
(4)解:如图4,∵∠BPC=60°保持不变,
因此点P在一圆弧上运动.
此圆是以K为圆心(K在BC的垂直平分线上,且∠BKC=120°),BK为半径.
当BP为直径时,BP最大.
在Rt△PCR中可求得PR=1,RC= ![]() .
.
所以点P的坐标为(1,2 ![]() ).
).
【解析】解:(1)当y=0时,x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
当x=0时,y=3,
∴A(﹣1,0),B(3,0),OD=3,
如图1,连接MC,由题意得,OM=1,MC=2,
∴OC= ![]() =
= ![]() ,
,
∴C(0, ![]() ),CD=3+
),CD=3+ ![]() ,
,
所以答案是:(﹣1,0);(3,0);(0, ![]() );3+
);3+ ![]() ;
;

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案