题目内容
已知：如图，⊙O1与⊙O2相交于点A和点B，AC∥O1O2，交⊙O1于点C，⊙O1的半径为5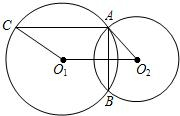
，⊙O2的半径为| 13 |
求：（1）弦AC的长度；
（2）四边形ACO1O2的面积．
分析：（1）作O1H⊥AC，垂足为点H．根据相交两圆的连心线垂直平分两圆的公共弦和平行线的性质，求得O1H的长，再进一步根据勾股定理和垂径定理进行计算；
（2）根据梯形的面积公式进行计算．
（2）根据梯形的面积公式进行计算．
解答：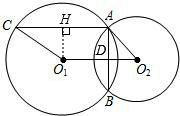
解：（1）作O1H⊥AC，垂足为点H，那么可得AH=CH．
∵⊙O1与⊙O2相交于点A和点B，
∴O1O2垂直平分AB，记垂足为D．
由题意，可证得四边形ADO1H是矩形．
又由AB=6，可得O1H=
AB=3．
∵O1C=5，
∴CH=4，
∴AC=8．
（2）在Rt△ADO2中，AO2=
，AD=3，
∴DO2=2．
而DO1=AH=4，
∴O1O2=6．
∴梯形ACO1O2的面积是S=
(8+6)×3=21．
解：（1）作O1H⊥AC，垂足为点H，那么可得AH=CH．∵⊙O1与⊙O2相交于点A和点B，
∴O1O2垂直平分AB，记垂足为D．
由题意，可证得四边形ADO1H是矩形．
又由AB=6，可得O1H=
| 1 |
| 2 |
∵O1C=5，
∴CH=4，
∴AC=8．
（2）在Rt△ADO2中，AO2=
| 13 |
∴DO2=2．
而DO1=AH=4，
∴O1O2=6．
∴梯形ACO1O2的面积是S=
| 1 |
| 2 |
点评：此题综合运用了相交两圆的性质、垂径定理和勾股定理．
练习册系列答案
相关题目
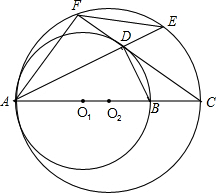O1于点D，AD的延长线交⊙O2于点E，连接AF、EF、BD．
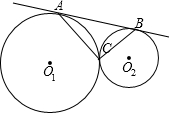已知：如图，⊙O1与⊙O2外切于C点，AB一条外公切线，A、B分别为切点，连接AC、BC．设⊙O1的半径为R，⊙O2的半径为r，若tan∠ABC=
（1998•南京）已知，如图，⊙O1与⊙O2相交，点P是其中一个交点，点A在⊙O2上，AP的延长线交⊙O1于点B，AO2的延长线交⊙O1于点C、D，交⊙O2于点E，连接PC、PE、PD，且
已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．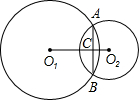
已知：如图，⊙O1与⊙O2相交于A、B，若两圆半径分别为12和5，O1O2=13，则AB=