Question

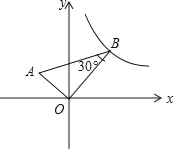
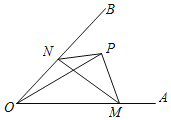
【题目】如图，正比例函数的图象与反比例函数在第一象限的图象交于点，过点作轴的垂线，垂足为点，且的面积为．若点为反比例函数在第一象限图象上的一点，点在轴上，且使最小，则点的坐标为________．

Answer 1

【答案】（，0）

【解析】

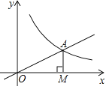
首先根据反比例函数中比例系数k的几何意义求得解析式，即可求得A、B的坐标，作出A关于x轴的对称点A′，直线BA′与x轴的交点就是P点，利用待定系数法即可求得BA′的解析式，即可求解．

解：∵△OAM的面积为1，
∴反比例函数y＝(k≠0)的解析式是：y=．
把x=1代入得：y=m=2，则B的坐标是（1，2）．
解方程组：，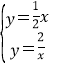
解得：x=2，y=1．
则A的坐标是（2，1）．
A关于x轴的对称点A′的坐标是（2，-1）．
设直线A′B的解析式是：y=kx+b，根据题意得： ，
解得： ，
则直线的解析式是：y=-3x+5．
令y=0得：x= ，则P的坐标是：（，0）．
故答案是：（，0）.