题目内容
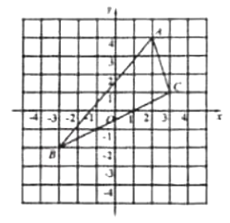
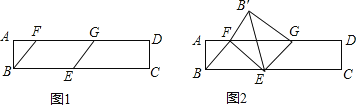
【题目】如图1,矩形ABCD中,AB=![]() ,BC=9,点E在BC边上,BE=4,点F,G在线段AD上运动(点F在点G的左侧),且始终保持FG=BE.
,BC=9,点E在BC边上,BE=4,点F,G在线段AD上运动(点F在点G的左侧),且始终保持FG=BE.
(1)求证:四边形BEGF是平行四边形;
(2)当四边形BEGF是菱形时,求线段DG的长;
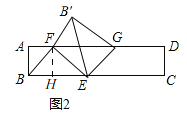
(3)将△BEF沿EF折叠得到△B′EF,连结B′G(如图2),当以点B′,G,E,F为顶点的四边形是矩形时,直接写出线段DG的长.
【答案】(1)见解析;(2)DG=5![]() ;(3)DG=1或2或4
;(3)DG=1或2或4
【解析】
(1)根据矩形的性质得出AD∥BC,即可得出四边形BEGF是平行四边形;
(2)根据菱形的性质得出BF=FG=BE=4,再用勾股定理即可;
(3)分两种情况讨论,①当BF⊥EF,由直角三角形的面积得出EFBF=4![]() ,再利用勾股定理得出BF2+EF2=16,联立方程组求出BF,再用勾股定理求出AF即可,②当EF⊥BC时,四边形ABEF是矩形,即可求出DG的长度.
,再利用勾股定理得出BF2+EF2=16,联立方程组求出BF,再用勾股定理求出AF即可,②当EF⊥BC时,四边形ABEF是矩形,即可求出DG的长度.
(1)∵四边形ABCD是矩形,
∴AD∥BC,
∵FG=BE,
∴四边形BEGF是平行四边形;
(2)∵四边形ABCD是矩形,
∴AD=BC=9,∠BAD=90°,
∵四边形BEGF是菱形,
∴BF=FG=BE=4,
在Rt△ABF中,AF=![]() =
=![]() ;
;
∴DG=ADAFFG=94![]() =5
=5![]() ;
;
(3)∵△BEF沿EF折叠得到△B'EF,
∴∠BFE=∠B'FE,
∵点B′,G,E,F为顶点的四边形是矩形,
①当BF⊥EF,过点F作FH⊥BC于H,
∴∠BFE=∠B'FE=90°,
∴FH=![]() ,
,
∵BE=4,
根据直角三角形的面积得,EFBF=ABBE=4![]()
在Rt△BEF中,BF2+EF2=16
解得:BF=2或BF=2![]() ,
,
当BF=2时,根据勾股定理得,AF=1,
DG=ADAFFG=914=4,
当BF=2![]() ,根据勾股定理得,AF=3,
,根据勾股定理得,AF=3,
∴DG=ADAFFG=934=2.
即:DG=2或4.
②当EF⊥BC时,四边形ABEF是矩形,
∴AF=BE=4,
∵FG=BE=4,
∴DG=ADAFFG=1,
即:DG=1或2或4.

 阅读快车系列答案
阅读快车系列答案【题目】某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
销售额(万元) | 17 | 19 | 20 | 21 | 25 | 26 | 28 | 30 |
频数(人数) | 1 | 1 | 3 | 3 |
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.