题目内容
(2011?金华)如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是_______.

2 .
.
 .
.根据平行四边形的性质得到AB=CD=3,AD=BC=4,求出BE、BF、EF,根据相似得出CH=1,EH= 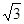 ,根据三角形的面积公式求△DFH的面积,即可求出答案.
,根据三角形的面积公式求△DFH的面积,即可求出答案.
解:∵四边形ABCD是平行四边形,
∴AD=BC=4,AB∥CD,AB=CD=3,
∵E为BC中点,
∴BE=CE=2,
∵∠B=60°,EF⊥AB,
∴∠FEB=30°,
∴BF=1,
由勾股定理得:EF=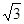 ,
,
∵AB∥CD,
∴△BFE∽△CHE,
EF:EH=BE:CE=BF:CH=1:1,
∴EF=EH=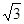 ,CH=BF=1,
,CH=BF=1,
∵S△DHF=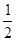 DH?FH=4
DH?FH=4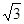 ,
,
∴S△DEF=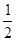 S△DHF=2
S△DHF=2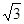 .
.
本题主要考查对平行四边形的性质,平行线的性质,勾股定理,含30度角的直角三角形,三角形的面积,三角形的内角和定理等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.
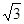 ,根据三角形的面积公式求△DFH的面积,即可求出答案.
,根据三角形的面积公式求△DFH的面积,即可求出答案.解:∵四边形ABCD是平行四边形,
∴AD=BC=4,AB∥CD,AB=CD=3,
∵E为BC中点,
∴BE=CE=2,
∵∠B=60°,EF⊥AB,
∴∠FEB=30°,
∴BF=1,
由勾股定理得:EF=
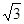 ,
,∵AB∥CD,
∴△BFE∽△CHE,
EF:EH=BE:CE=BF:CH=1:1,
∴EF=EH=
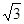 ,CH=BF=1,
,CH=BF=1,∵S△DHF=
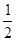 DH?FH=4
DH?FH=4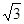 ,
,∴S△DEF=
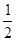 S△DHF=2
S△DHF=2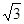 .
.本题主要考查对平行四边形的性质,平行线的性质,勾股定理,含30度角的直角三角形,三角形的面积,三角形的内角和定理等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.
面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化. (不要求写出自变量x的取值范围);
(不要求写出自变量x的取值范围);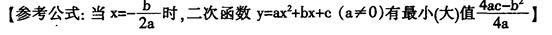

 果DE2=BE·CE,求证四边形ABFC是矩形.
果DE2=BE·CE,求证四边形ABFC是矩形.


 。
。
 毛
毛