题目内容
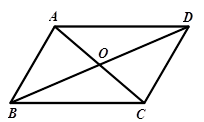
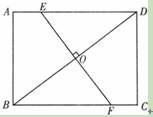
(本题满分12分,每小题满分各6分)如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.联结BF、CD、AC.
(1)求证:四边形ABFC是平行四边形;
(2)如 果DE2=BE·CE,求证四边形ABFC是矩形.
果DE2=BE·CE,求证四边形ABFC是矩形.
(1)求证:四边形ABFC是平行四边形;
(2)如
 果DE2=BE·CE,求证四边形ABFC是矩形.
果DE2=BE·CE,求证四边形ABFC是矩形.
(本题满分12分,每小题满分各6分)
[解] (1) 等腰梯形ABCD中,AB=DC,ÐB=ÐDCB,∵△DFC是等腰三角形,∴ÐDCB=ÐFCE,
DC=CF,所以ÐB=ÐFCE,AB=CF,易证四边形ABFC是平行四边形。
(2) 提示:射影定理的逆定理不能直接在中考中使用,必须通过相似三角形来证明,内角为90°。
[解] (1) 等腰梯形ABCD中,AB=DC,ÐB=ÐDCB,∵△DFC是等腰三角形,∴ÐDCB=ÐFCE,
DC=CF,所以ÐB=ÐFCE,AB=CF,易证四边形ABFC是平行四边形。
(2) 提示:射影定理的逆定理不能直接在中考中使用,必须通过相似三角形来证明,内角为90°。
略

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目


 ,∠A=60°,E为
,∠A=60°,E为 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点 处,过点
处,过点 处,
处,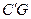 与
与 与
与 于点M、N.若点
于点M、N.若点 (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.




 ,若重叠四边形
,若重叠四边形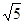 -1)cm B、
-1)cm B、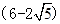 cm
cm 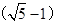 cm D、
cm D、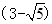 cm
cm