题目内容
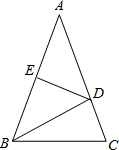
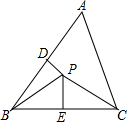
如图，△ABC中∠A=56°，PD垂直平分AB，PE垂直平分BC，则∠BPC的度数为（ ）
| A．124° | B．112° | C．108° | D．118° |
如图，连接PA，∵PD垂直平分AB，PE垂直平分BC，
∴PA=PB，PB=PC，
∴PA=PB=PC，
∴∠PBA=∠PAB，∠PCA=∠PAC，
∵∠A=56°，
∴∠PBA+∠PCA=∠PAB+∠PAC=∠A=56°，
在△ABC中，∠PBC+∠PCB=180°-∠A-（∠PBA+∠PCA）=180°-56°-56°=68°，
在△PBC中，∠BPC=180°-（∠PBC+∠PCB）=180°-68°=112°．
故选B．
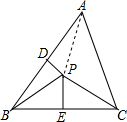
∴PA=PB，PB=PC，
∴PA=PB=PC，
∴∠PBA=∠PAB，∠PCA=∠PAC，
∵∠A=56°，
∴∠PBA+∠PCA=∠PAB+∠PAC=∠A=56°，
在△ABC中，∠PBC+∠PCB=180°-∠A-（∠PBA+∠PCA）=180°-56°-56°=68°，
在△PBC中，∠BPC=180°-（∠PBC+∠PCB）=180°-68°=112°．
故选B．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
