题目内容
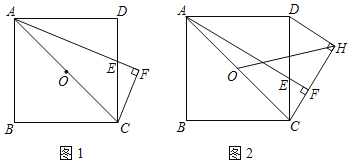
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论.

【答案】(1)DM⊥EM,DM=EM,见解析;(2)DM⊥EM,DM=EM,见解析.
【解析】
(1)根据全等三角形的性质推出MH=ME,AH=EF=EC,推出DH=DE,因为∠EDH=90°,可得DM⊥EM,DM=ME;
(2)结论不变,延长EM交DA的延长线于H,由正方形的性质和平行线的性质,得到边和角的关系,可以证明△AMH≌△FME,然后得到MH=ME,AH=EF=EC,进而得到结论.
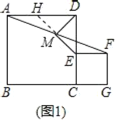
解:(1)结论:DM⊥EM,DM=EM.
理由:如图1中,延长EM交AD于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME(AAS),
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME;
(2)如图2中,结论不变.DM⊥EM,DM=EM.
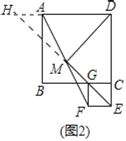
理由:如图2中,延长EM交DA的延长线于H.
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
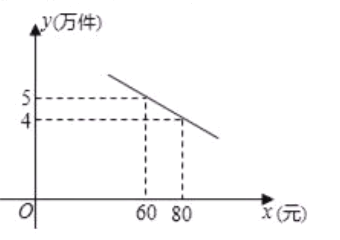
冲刺100分单元优化练考卷系列答案【题目】河西王府井销售一种 T 恤衫,每件进价为 40 元,经过市场调查,一周的销售量y 件与销售单价 x 元/件满足某种函数关系:
销售单价 x (元/件) | 50 | 60 | 70 | 80 | ||
一周的销售量 y(件) | 350 | 300 | 250 | 200 |
(1)请根据所学的知识,选择合适的函数模型,求出 y 与 x 的之间的函数关系式;
(2)设一周的销售利润为 w 元,请求出 w 与 x 的函数关系式,并确定当销售单价为多少时一周的销售利润最大,并求出最大利润;
(3)商场决定将一周销售 T 恤衫的利润全部捐给某村用于精准扶贫的水网改造项目,在商场购进该T 恤衫的资金不超过 6000 元情况下,请求出该商场最大捐款数额是多少元?