题目内容
如图(1),E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为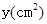 ,已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是( )
,已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是( )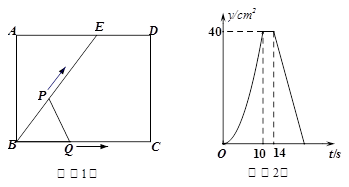
| A.AE=8 |
B.当0≤t≤10时,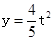 |
C.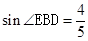 |
D.当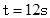 时,△BPQ是等腰三角形 时,△BPQ是等腰三角形 |
D.
解析试题分析:由图2可知,在点(10,40)至点(14,40)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下:(1)在BE段,BP=BQ;持续时间10s,则BE=BC=10;y是t的二次函数;(2)在ED段,y=40是定值,持续时间4s,则ED=4;(3)在DC段,y持续减小直至为0,y是t的一次函数.
(1)结论A正确.理由如下:
分析函数图象可知,BC=10cm,ED=4cm,故AE=AD-ED=BC-ED=10-4=6cm;
(2)结论B正确.理由如下:
如图1所示,连接EC,过点E作EF⊥BC于点F,
由函数图象可知,BC=BE=10cm,S△BEC=40= BC•EF=
BC•EF= ×10×EF,∴EF=8,
×10×EF,∴EF=8,
∴sin∠EBC= ;
;
(3)结论C正确.理由如下:
如图2所示,过点P作PG⊥BQ于点G,
∵BQ=BP=t,∴y=S△BPQ= BQ•PG=
BQ•PG= BQ•BP•sin∠EBC=
BQ•BP•sin∠EBC= t•t•
t•t• =
= t2.
t2.
(4)结论D错误.理由如下:
当t=12s时,点Q与点C重合,点P运动到ED的中点,设为N,如图3所示,连接NB,NC.
此时AN=8,ND=2,由勾股定理求得:NB= ,NC=
,NC= ,
,
∵BC=10,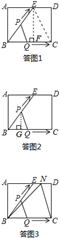
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形
考点:动点问题的函数图象.

二次函数y=2(x+1)2-3的图象的对称轴是( )
| A.直线x=-1 | B.直线x=1 | C.直线x=-3 | D.直线x=3 |
如图,二次函数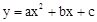 的图象过(1,-1)和(3,0),则下列关于这个二次函数的描述,正确的是( ).
的图象过(1,-1)和(3,0),则下列关于这个二次函数的描述,正确的是( ).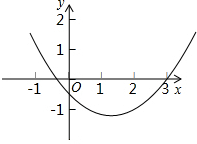
| A.y的最小值大于-1 | B.当x=0时,y的值大于0 |
| C.当x=2时,y的值等于-1 | D.当x>3时,y的值大于0 |
将二次函数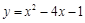 化为
化为 的形式,结果为( )
的形式,结果为( )
A. | B.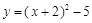 |
C.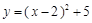 | D.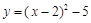 |
将抛物线y=3x2向右平移2个单位,则新抛物线的解析式是
A.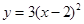 | B.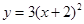 |
C.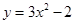 | D.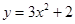 |
二次函数 (a≠0)的图像如图所示,若
(a≠0)的图像如图所示,若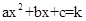 (k≠0)有两个不相等的实数根,则k的取值范围是( )
(k≠0)有两个不相等的实数根,则k的取值范围是( ) 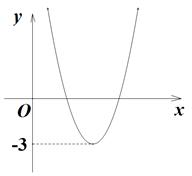
A.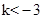 | B.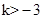 | C. | D. |

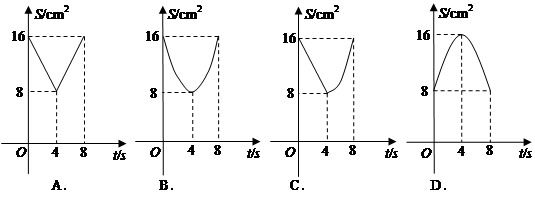
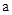 ,则这两个正方形的面积的和S关于
,则这两个正方形的面积的和S关于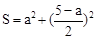
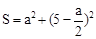


 的图象可能是( )
的图象可能是( )