Question

【题目】如图，点A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OF⊥OA交圆O于点F，则∠CBF等于（ ）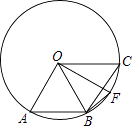
A.12.5°
B.15°
C.20°
D.22.5°

Answer 1

【答案】B
【解析】解：∵四边形ABCO是平行四边形， ∴AB=BC，OA∥BC．
∵OA=OC，
∴△OAB是等边三角形，
∴∠AOB=60°．
∵OF⊥OA，
∴∠AOF=90°，OF⊥BC，
∴∠BOF=∠COF=90°﹣60°=30°，
∴∠CBF= ∠COF=15°．
故选B．
【考点精析】通过灵活运用平行四边形的性质和垂径定理，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧即可以解答此题．