题目内容
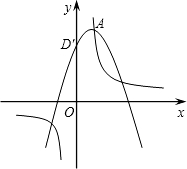
如图,已知抛物线C1的解析式为y=-x2+2x+8,图象与y轴交于D点,并且顶点A在双曲线上.(1)求过顶点A的双曲线解析式;
(2)若开口向上的抛物线C2与C1的形状、大小完全相同,并且C2的顶点P始终在C1上,证明:抛物线C2一定经过A点;
(3)设(2)中的抛物线C2的对称轴PF与x轴交于F点,且与双曲线交于E点,当D、O、E
 、F四点组成的四边形的面积为16.5时,先求出P点坐标,并在直线y=x上求一点M,使|MD-MP|的值最大.
、F四点组成的四边形的面积为16.5时,先求出P点坐标,并在直线y=x上求一点M,使|MD-MP|的值最大.
分析:(1)把抛物线C1的解析式化为顶点式即可求出A点坐标,再用待定系数法求出经过A点的双曲线解析式即可;
(2)设抛物线C2的顶点P的坐标为(m,n),由点P(m,n)在抛物线C1上可得出n、m的解析式,再根据C1与C2的形状、大小完全相同,开口向上,可设出抛物线C2的解析式,令x=1即可得出抛物线C2必经过得点;
(3)设抛物线C2的对称轴为x=m,则OF=|m|,EF=|
|,由抛物线C1的解析式求出D点坐标,再根据由D、O、E、F四点组成的四边形是梯形,由梯形的面积公式即可求出m的值,进而可求出P1、P2两点的坐标;
①当点D、P1在直线y=x的同侧,连接P1D交直线y=x于点M1,则M1点即为所求点,用待定系数法求出过D、P1两点的直线解析式,根据此解析式与y=x有交点即可求出M1点的坐标;
②点D、P2在直线y=x的异侧,D点关于直线y=x的对称点为D′(8,0),连接D′P2交直线y=x于M2点,则M2点即为所求点,用待定系数法求出过D、P2两点的直线解析式,根据此解析式与y=x有交点即可求出M2点的坐标,进而即可得出结论.
(2)设抛物线C2的顶点P的坐标为(m,n),由点P(m,n)在抛物线C1上可得出n、m的解析式,再根据C1与C2的形状、大小完全相同,开口向上,可设出抛物线C2的解析式,令x=1即可得出抛物线C2必经过得点;
(3)设抛物线C2的对称轴为x=m,则OF=|m|,EF=|
| 9 |
| m |
①当点D、P1在直线y=x的同侧,连接P1D交直线y=x于点M1,则M1点即为所求点,用待定系数法求出过D、P1两点的直线解析式,根据此解析式与y=x有交点即可求出M1点的坐标;
②点D、P2在直线y=x的异侧,D点关于直线y=x的对称点为D′(8,0),连接D′P2交直线y=x于M2点,则M2点即为所求点,用待定系数法求出过D、P2两点的直线解析式,根据此解析式与y=x有交点即可求出M2点的坐标,进而即可得出结论.
解答:解:(1)由抛物线C1的解析式可得,y=-(x-1)2+9,
∴顶点A的坐标为(1,9)
设图象经过点A(1,9)的反比例函数解析式为y=
(k≠0),
把x=1,y=9代入得9=
,
解得k=9,
∴图象经过点A(1,9)的反比例函数的解析式为y=
;
(2)设抛物线C2的顶点P的坐标为(m,n),
∵点P(m,n)在抛物线C1上,
∴n=-m2+2m+8,
又∵C1与C2的形状、大小完全相同,开口向上,
∴可设抛物线C2的解析式为y=(x-m)2+(-m2+2m+8)=x2-2mx+2m+8,
∴当x=1时,由抛物线C2的解析式得,y=1-2m+2m+8=9,
∴抛物线C2必经过A(1,9)点;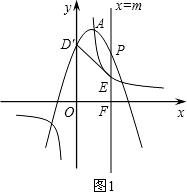
(3)如图1,设抛物线C2的对称轴为x=m,则OF=|m|,EF=|
|,
由抛物线C1的:y=-x2+2x+8得,D点坐标为(0,8),
∵由D、O、E、F四点组成的四边形是梯形,
∴(8+|
|)×|m|×
=16.5,解得m=±3,
当m=3时,n=-m2+2m+8=-32+2×3+8=5,
∴P1(3,5);
当m=-3时,n=-m2+2m+8=-(-3)2+2×(-3)+8=-7,
∴P2(-3,-7),
①如图2,点D、P1在直线y=x的同侧,连接P1D交直线y=x于点M1,则M1点即为所求点.
∵过D(0,8)、P1(3,5)两点的直线解析式为y=-x+8,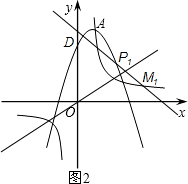
由方程组
得
;
∴M1(4,4);
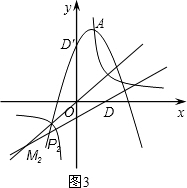
②如图3,点D、P2在直线y=x的异侧,D点关于直线y=x的对称点为D′(8,0),
连接D′P2交直线y=x于M2点,则M2点即为所求点.
∵过D′(8,0)、P2(-3,-7)两点的直线解析式为y=
x-
,
由方程组
得,
,
∴M2(-14,-14).
综上所述,当M点为(4,4)或(-14,-14)时,使得|MD-MP|的值最大.
∴顶点A的坐标为(1,9)
设图象经过点A(1,9)的反比例函数解析式为y=
| k |
| x |
把x=1,y=9代入得9=
| k |
| 1 |
解得k=9,
∴图象经过点A(1,9)的反比例函数的解析式为y=
| 9 |
| x |
(2)设抛物线C2的顶点P的坐标为(m,n),
∵点P(m,n)在抛物线C1上,
∴n=-m2+2m+8,
又∵C1与C2的形状、大小完全相同,开口向上,
∴可设抛物线C2的解析式为y=(x-m)2+(-m2+2m+8)=x2-2mx+2m+8,
∴当x=1时,由抛物线C2的解析式得,y=1-2m+2m+8=9,
∴抛物线C2必经过A(1,9)点;

(3)如图1,设抛物线C2的对称轴为x=m,则OF=|m|,EF=|
| 9 |
| m |
由抛物线C1的:y=-x2+2x+8得,D点坐标为(0,8),
∵由D、O、E、F四点组成的四边形是梯形,
∴(8+|
| 9 |
| m |
| 1 |
| 2 |
当m=3时,n=-m2+2m+8=-32+2×3+8=5,
∴P1(3,5);
当m=-3时,n=-m2+2m+8=-(-3)2+2×(-3)+8=-7,
∴P2(-3,-7),
①如图2,点D、P1在直线y=x的同侧,连接P1D交直线y=x于点M1,则M1点即为所求点.
∵过D(0,8)、P1(3,5)两点的直线解析式为y=-x+8,

由方程组
|
|
∴M1(4,4);

②如图3,点D、P2在直线y=x的异侧,D点关于直线y=x的对称点为D′(8,0),
连接D′P2交直线y=x于M2点,则M2点即为所求点.
∵过D′(8,0)、P2(-3,-7)两点的直线解析式为y=
| 7 |
| 11 |
| 56 |
| 11 |
由方程组
|
|
∴M2(-14,-14).
综上所述,当M点为(4,4)或(-14,-14)时,使得|MD-MP|的值最大.
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式、待定系数法求反比例函数的解析式及一次函数的解析式,涉及面较广,难度较大.

练习册系列答案
相关题目
 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;