题目内容
如图,已知抛物线c1:y=-
x2+bx+c与x轴交于点A、B(点A在B的左侧),与y轴交于点C,抛物线c2与抛物线c1关于y轴对称,点A、B的对称点分别是E、D,连接CD、CB,设AD=m.
(1)抛物线c2可以看成抛物线c1向右平移
(2)若m=2,求b的值.
(3)将△CDB沿直线BC折叠,点D的对应点为G,且四边形CDBG是平行四边形,
①△CDB为
②若点G恰好落在抛物线c2上,求m的值.

| 1 | 4 |
(1)抛物线c2可以看成抛物线c1向右平移
m
m
个单位得到.(2)若m=2,求b的值.
(3)将△CDB沿直线BC折叠,点D的对应点为G,且四边形CDBG是平行四边形,
①△CDB为
等边
等边
三角形(按边分);②若点G恰好落在抛物线c2上,求m的值.

分析:(1)对于抛物线c1上的A点来说,当c1平移到c2时,点A运动到点D,因此c2可看作c1向右平移AD长(即m)个单位得到.
(2)c2、c1关于y轴对称,所以它们的开口方向、开口大小相同,与y轴交点相同,唯一不同的是对称轴关于y轴对称,所以两个解析式的二次项和常数项系数相同,不同的是一次项系数互为相反数,可据此设出c2的函数解析式,则它们的对称轴的差的绝对值即为m的值,由此求出b.
(3)①由题意不难判断B、D关于y轴对称,那么△CBD首先是个等腰三角形,即∠CDB=∠CBD,而四边形CDBG是平行四边形,即∠GCB=∠CBD;△GCB由△DCB翻折所得,所以∠GCB=∠DCB=∠CBD,即△CDB的三个内角相等,因此这个三角形应该是等边三角形;
②这道小题要用到(2)、(3)①的结论,首先由(2)的结论用m、c表示出c2的解析式,在等边△CDB中,OC=c,那么OD、OB的长也可由c表示出来,所以可以得到B、D的坐标(用c来表示),而CG∥x轴,且CG=BD,所以用c也可表达出G点的坐标,将G、D两点的坐标代入c2的解析式中,即可求出m的值.
(2)c2、c1关于y轴对称,所以它们的开口方向、开口大小相同,与y轴交点相同,唯一不同的是对称轴关于y轴对称,所以两个解析式的二次项和常数项系数相同,不同的是一次项系数互为相反数,可据此设出c2的函数解析式,则它们的对称轴的差的绝对值即为m的值,由此求出b.
(3)①由题意不难判断B、D关于y轴对称,那么△CBD首先是个等腰三角形,即∠CDB=∠CBD,而四边形CDBG是平行四边形,即∠GCB=∠CBD;△GCB由△DCB翻折所得,所以∠GCB=∠DCB=∠CBD,即△CDB的三个内角相等,因此这个三角形应该是等边三角形;
②这道小题要用到(2)、(3)①的结论,首先由(2)的结论用m、c表示出c2的解析式,在等边△CDB中,OC=c,那么OD、OB的长也可由c表示出来,所以可以得到B、D的坐标(用c来表示),而CG∥x轴,且CG=BD,所以用c也可表达出G点的坐标,将G、D两点的坐标代入c2的解析式中,即可求出m的值.
解答:解:(1)抛物线c1图象上的A点向右平移m个单位后,得到抛物线c2图象上的D点,故抛物线c2可由抛物线c1向右平移m个单位得到;
故填:m.
(2)抛物线c1、c2关于y轴对称,
已知,抛物线c1:y=-
x2+bx+c,对称轴:x=2b;
则,抛物线c2:y=-
x2-bx+c,对称轴:x=-2b;
由(1)知:抛物线c2可由抛物线c1向右平移m个单位得到,则:
-2b-2b=m,即:b=-
=-
.
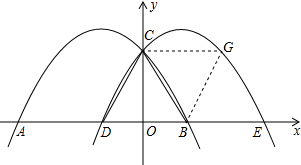 (3)①如右图,若四边形CDBG是平行四边形,则∠GCB=∠CBD;
(3)①如右图,若四边形CDBG是平行四边形,则∠GCB=∠CBD;
已知,△GCB由△DCB翻折所得,故∠GCB=∠DCB;
∴∠DCB=∠CBD;
由题意,知:B、D关于y轴对称,所以CB=CD,即:∠CDB=∠CBD;
∴∠DCB=∠DCB=∠CBD,即△CDB是等边三角形;
②在等边△CBD中,OB=OD,∠CDO=60°,OC=c,则:OD=OB=
c,即:D(-
c,0);
∵CG∥x轴,且CG=BD=
c,
∴G(
c,c);
由(2)的结论,可设抛物线c2:y=-
x2+
x+c,代入D、G两点的坐标,得:
解得:m=
.
故填:m.
(2)抛物线c1、c2关于y轴对称,
已知,抛物线c1:y=-
| 1 |
| 4 |
则,抛物线c2:y=-
| 1 |
| 4 |
由(1)知:抛物线c2可由抛物线c1向右平移m个单位得到,则:
-2b-2b=m,即:b=-
| m |
| 4 |
| 1 |
| 2 |
 (3)①如右图,若四边形CDBG是平行四边形,则∠GCB=∠CBD;
(3)①如右图,若四边形CDBG是平行四边形,则∠GCB=∠CBD;已知,△GCB由△DCB翻折所得,故∠GCB=∠DCB;
∴∠DCB=∠CBD;
由题意,知:B、D关于y轴对称,所以CB=CD,即:∠CDB=∠CBD;
∴∠DCB=∠DCB=∠CBD,即△CDB是等边三角形;
②在等边△CBD中,OB=OD,∠CDO=60°,OC=c,则:OD=OB=
| ||
| 3 |
| ||
| 3 |
∵CG∥x轴,且CG=BD=
2
| ||
| 3 |
∴G(
2
| ||
| 3 |
由(2)的结论,可设抛物线c2:y=-
| 1 |
| 4 |
| m |
| 4 |
|
解得:m=
8
| ||
| 3 |
点评:此题主要考查的是二次函数图象的平移、图形的对称和翻折以及平行四边形的性质;抛物线在对称或平移过程中,解析式中各系数的变化情况是需要牢固掌握的地方;难度较大.

练习册系列答案
相关题目
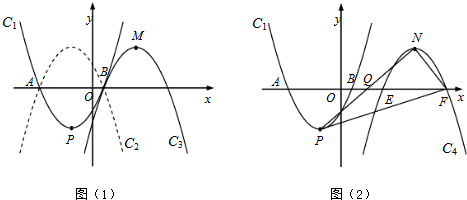

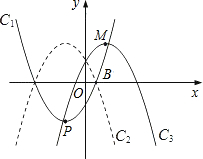 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;