题目内容
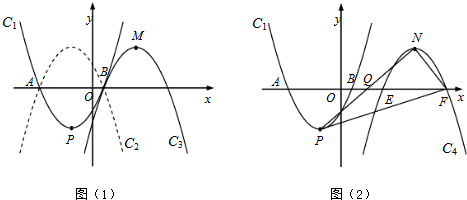
如图,已知抛物线C1:y=a(x+2)2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.(1)求P点坐标及a的值;
(2)如图(1),抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
(3)如图(2),点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
分析:(1)由抛物线C1:y=a(x+2)2-5得顶点P的为(-2,-5),把点B(1,0)代入抛物线解析式,解得,a=
;
(2)连接PM,作PH⊥x轴于H,作MG⊥x轴于G,根据点P、M关于点B成中心对称,证明△PBH≌△MBG,所以MG=PH=5,BG=BH=3,即顶点M的坐标为(4,5),根据抛物线C2由C1关于x轴对称得到,抛物线C3由C2平移得到,所以抛物线C3的表达式为y=-
(x-4)2+5;
(3)根据抛物线C4由C1绕点x轴上的点Q旋转180°得点N的纵坐标为5,设点N坐标为(m,5),作PH⊥x轴于H,作NG⊥x轴于G,作PK⊥NG于K,可求得EF=AB=2BH=6,FG=3,点F坐标为(m+3,0),H坐标为(2,0),K坐标为(m,-5),根据勾股定理得:PN2=NK2+PK2=m2+4m+104,PF2=PH2+HF2=m2+10m+50,NF2=52+32=34.
分三种情况讨论,利用勾股定理列方程求解即可.①当2∠PNF=90°时,PN2+NF2=PF2,解得m=
,即Q点坐标为(
,0);②当∠PFN=90°时,PF2+NF2=PN2,解得m=
,∴Q点坐标为(
,0),③PN>NK=10>NF,所以∠NPF≠90°综上所得,当Q点坐标为(
,0)或(
,0)时,以点P、N、F为顶点的三角形是直角三角形.
| 5 |
| 9 |
(2)连接PM,作PH⊥x轴于H,作MG⊥x轴于G,根据点P、M关于点B成中心对称,证明△PBH≌△MBG,所以MG=PH=5,BG=BH=3,即顶点M的坐标为(4,5),根据抛物线C2由C1关于x轴对称得到,抛物线C3由C2平移得到,所以抛物线C3的表达式为y=-
| 5 |
| 9 |
(3)根据抛物线C4由C1绕点x轴上的点Q旋转180°得点N的纵坐标为5,设点N坐标为(m,5),作PH⊥x轴于H,作NG⊥x轴于G,作PK⊥NG于K,可求得EF=AB=2BH=6,FG=3,点F坐标为(m+3,0),H坐标为(2,0),K坐标为(m,-5),根据勾股定理得:PN2=NK2+PK2=m2+4m+104,PF2=PH2+HF2=m2+10m+50,NF2=52+32=34.
分三种情况讨论,利用勾股定理列方程求解即可.①当2∠PNF=90°时,PN2+NF2=PF2,解得m=
| 44 |
| 3 |
| 19 |
| 3 |
| 10 |
| 3 |
| 2 |
| 3 |
| 19 |
| 3 |
| 2 |
| 3 |
解答: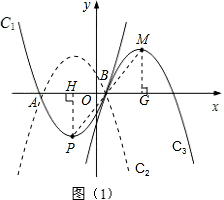 解:(1)由抛物线C1:y=a(x+2)2-5得,
解:(1)由抛物线C1:y=a(x+2)2-5得,
顶点P的坐标为(-2,-5),
∵点B(1,0)在抛物线C1上,
∴0=a(1+2)2-5,
解得a=
;
(2)连接PM,作PH⊥x轴于H,作MG⊥x轴于G,
∵点P、M关于点B成中心对称,
∴PM过点B,且PB=MB,
∴△PBH≌△MBG,
∴MG=PH=5,BG=BH=3,
∴顶点M的坐标为(4,5),
抛物线C2由C1关于x轴对称得到,抛物线C3由C2平移得到,
∴抛物线C3的表达式为y=-
(x-4)2+5;
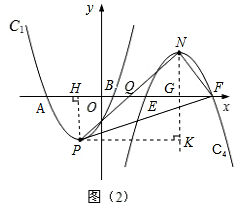
(3)∵抛物线C4由C1绕点x轴上的点Q旋转180°得到,
∴顶点N、P关于点Q成中心对称,
由(2)得点N的纵坐标为5,
设点N坐标为(m,5),
作PH⊥x轴于H,作NG⊥x轴于G,
作PK⊥NG于K,
∵旋转中心Q在x轴上,
∴EF=AB=2BH=6,
∴FG=3,点F坐标为(m+3,0).
H坐标为(-2,0),K坐标为(m,-5),
∵顶点P的坐标为(-2,-5),
根据勾股定理得:
PN2=NK2+PK2=m2+4m+104,
PF2=PH2+HF2=m2+10m+50,
NF2=52+32=34,
①当∠PNF=90°时,PN2+NF2=PF2,解得m=
,
∴Q点坐标为(
,0).
②当∠PFN=90°时,PF2+NF2=PN2,解得m=
,
∴Q点坐标为(
,0).
③∵PN>NK=10>NF,
∴∠NPF≠90°
综上所得,当Q点坐标为(
,0)或(
,0)时,以点P、N、F为顶点的三角形是直角三角形.
 解:(1)由抛物线C1:y=a(x+2)2-5得,
解:(1)由抛物线C1:y=a(x+2)2-5得,顶点P的坐标为(-2,-5),
∵点B(1,0)在抛物线C1上,
∴0=a(1+2)2-5,
解得a=
| 5 |
| 9 |
(2)连接PM,作PH⊥x轴于H,作MG⊥x轴于G,
∵点P、M关于点B成中心对称,
∴PM过点B,且PB=MB,
∴△PBH≌△MBG,
∴MG=PH=5,BG=BH=3,
∴顶点M的坐标为(4,5),
抛物线C2由C1关于x轴对称得到,抛物线C3由C2平移得到,
∴抛物线C3的表达式为y=-
| 5 |
| 9 |

(3)∵抛物线C4由C1绕点x轴上的点Q旋转180°得到,
∴顶点N、P关于点Q成中心对称,
由(2)得点N的纵坐标为5,
设点N坐标为(m,5),
作PH⊥x轴于H,作NG⊥x轴于G,
作PK⊥NG于K,
∵旋转中心Q在x轴上,
∴EF=AB=2BH=6,
∴FG=3,点F坐标为(m+3,0).
H坐标为(-2,0),K坐标为(m,-5),
∵顶点P的坐标为(-2,-5),
根据勾股定理得:
PN2=NK2+PK2=m2+4m+104,
PF2=PH2+HF2=m2+10m+50,
NF2=52+32=34,
①当∠PNF=90°时,PN2+NF2=PF2,解得m=
| 44 |
| 3 |
∴Q点坐标为(
| 19 |
| 3 |
②当∠PFN=90°时,PF2+NF2=PN2,解得m=
| 10 |
| 3 |
∴Q点坐标为(
| 2 |
| 3 |
③∵PN>NK=10>NF,
∴∠NPF≠90°
综上所得,当Q点坐标为(
| 19 |
| 3 |
| 2 |
| 3 |
点评:本题结合三角形的性质考查二次函数的综合应用,函数和几何图形的综合题目,要利用直角三角形的性质和二次函数的性质把数与形有机的结合在一起,利用勾股定理作为相等关系求解.

练习册系列答案
相关题目


 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;