题目内容
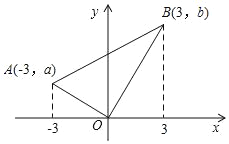
【题目】如图，在Rt△AOB中，∠AOB为直角，A（﹣3，a）、B（3，b），a+b﹣12=0，则△AOB的面积为_____．
【答案】18
【解析】
作AC⊥x轴于C，BD⊥x轴于D，根据三角形面积公式，利用S△AOB=S梯形ACDB﹣S△AOC﹣S△BOD可得到S△AOB=
（a+b），然后根据a+b﹣12=0可计算出△AOB的面积．
解：作AC⊥x轴于C，BD⊥x轴于D，
∵A（﹣3，a）、B（3，b），
∴AC=a，OC=3，OD=3，BD=b，
∴S△AOB=S梯形ACDB﹣S△AOC﹣S△BOD
=
（a+b）×6﹣×3×a﹣×3×b
=3（a+b）﹣（a+b）
=（a+b），
而a+b=12，
∴S△AOB=×12=18．
故答案为18．
练习册系列答案
相关题目
