题目内容
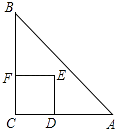
【题目】如图,将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE,连接BE,延长DE、BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.
(1)判断△ABE的形状,并证明你的结论;
(2)用含b代数式表示四边形ABFE的面积;
(3)求证:a2+b2=c2.

【答案】(1)△ABE是等腰直角三角形,证明详见解析;(2)b 2;(3)详见解析.
【解析】
(1)利用旋转的性质得出∠BAE=∠BAC+∠CAE=∠CAE+∠DAE=90°,AB=AE,即可得出△ABE的形状;(2)利用四边形ABFE的面积等于正方形ACFD面积,即可得出答案;(3)利用正方形ACFD面积等于Rt△BAE和Rt△BFE的面积之和进而证明即可.
(1)△ABE是等腰直角三角形,
证明:∵Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE,
∴∠BAC=∠DAE,
∴∠BAE=∠BAC+∠CAE=∠CAE+∠DAE=90°,
又∵AB=AE,
∴△ABE是等腰直角三角形;
(2)∵四边形ABFE的面积等于正方形ACFD面积,
∴四边形ABFE的面积等于:b 2.
(3)∵S正方形ACFD=S△BAE+S△BFE
即:b2=![]() c2+
c2+![]() (b+a)(b﹣a),
(b+a)(b﹣a),
整理:2b2=c2+(b+a)(b﹣a)
∴a2+b2=c2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目