Question

【题目】某数学小组对函数y1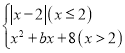＝图象和性质进行探究．当x＝4时，y1＝0．

（1）当x＝5时，求y1的值；

（2）在给出的平面直角坐标系中，补全这个函数的图象，并写出这个函数的一条性质；

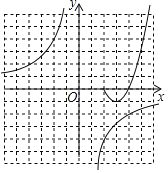
（3）进一步探究函数图象并解决问题：已知函数y2＝﹣的图象如图所示，结合函数y1的图象，直接写出不等式y1≥y2的解集．

Answer 1

【答案】（1）3；（2）画图象见解析；性质：x＜3时，y随x的增大而减小，x＞3时，y随x的增大而增大；（3）x＜﹣2或x＞0．

【解析】

（1）利用待定系数法确定b的值，再求出x＝5时，y1的值即可；

（2）画出x＜2时，y＝﹣x+2的图形即可；

（3）利用图象法写出y1的图象在y2的上方时x的值即可．

解：（1）由题意x＝0时，y1＝0，

∴16+4b+8＝0，

∴b＝﹣6，

∴x＝5时，y1＝25﹣6×5+8＝3．

（2）函数图象如图所示：

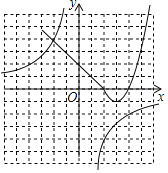
性质：x＜3时，y随x的增大而减小，x＞3时，y随x的增大而增大．

（3）观察图形可知：不等式y1≥y2的解集为：x＜﹣2或x＞0．