题目内容
九(1)班数学课题学习小组,为了研究学习二次函数问题,他们经历了实践——应用——探究的过程(1)实践:他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量,测得隧道的路面宽为10米,隧道顶部最高处距地面6.25米,并画出了隧道截面图,建立了如图所示的直角坐标系,请你求出抛物线的解析式
(2)应用:按规定机动车辆通过隧道时,车顶部与隧道顶部在竖起方向上的高度差至少为0.5米,为了确保安全,问该隧道能否让最宽3米,最高3.5米的两辆车居中并列行驶(不考虑两车之间的空隙)?
(3)探究:该课题学习小组为进一步探究抛物线的有关知识,他们借助上述抛物线模型,提出了以下两个问题,请予解答:
①如图,在抛物线内作矩形ABCD,使顶点C、D落在抛物线上,顶点A、B落在x轴上,设矩形ABCD的周长为为l,求l的最大值
②如图,过原点作一条直线y=x,交抛物线于M,交抛物线的对称轴于N,P为直线OM上一动点,过点P作x轴的垂线交抛物线于点Q,问在直线OM上是否存在点P,使以点P、N、Q为顶点的三角形为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由
 |
(1)y=-x2+x
(2)当x=2或x=8时
(3)(Ⅰ)AB="2x-10 " BC=y=-x2+x l=-x2+9x-20=-(x-9)2+
(Ⅱ)存在,这样的点有四个
∵P点在直线y=x上,设P(x,x),Q(x, -x2+x)
(A) 当∠P1Q1N=90°时,
Q点在OM的上方时,P1Q1=NQ1,P1Q1=-x2+x -x,NQ1=5-x
Q点在OM的下方时,P2Q2=NQ2,P2Q2= x-(-x2+x),NQ1="x" – 5
∴x2-x+5=0
∴P1(5+,5+)、P2(5-,5-)
(B) 当∠P3N Q3=90°时,过点Q3作Q3K⊥对称轴
当△NQ3K1为等腰直角三角形时,△NP3Q3为等腰直角三角形
Q点在OM的上方时,P3Q3=2Q3K1,P3Q3=-x2+x -x,Q3K1=5-x
Q点在OM的下方时,P4Q4=2Q4K2,P4Q4= x-(-x2+x),Q4K2=" x" – 5
∴x2-x+10=0
∴P3(4,4)、P4(10,10)解析:
略
(2)当x=2或x=8时
(3)(Ⅰ)AB="2x-10 " BC=y=-x2+x l=-x2+9x-20=-(x-9)2+
(Ⅱ)存在,这样的点有四个
∵P点在直线y=x上,设P(x,x),Q(x, -x2+x)
(A) 当∠P1Q1N=90°时,
Q点在OM的上方时,P1Q1=NQ1,P1Q1=-x2+x -x,NQ1=5-x
Q点在OM的下方时,P2Q2=NQ2,P2Q2= x-(-x2+x),NQ1="x" – 5
∴x2-x+5=0
∴P1(5+,5+)、P2(5-,5-)
(B) 当∠P3N Q3=90°时,过点Q3作Q3K⊥对称轴
当△NQ3K1为等腰直角三角形时,△NP3Q3为等腰直角三角形
Q点在OM的上方时,P3Q3=2Q3K1,P3Q3=-x2+x -x,Q3K1=5-x
Q点在OM的下方时,P4Q4=2Q4K2,P4Q4= x-(-x2+x),Q4K2=" x" – 5
∴x2-x+10=0
∴P3(4,4)、P4(10,10)解析:
略

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
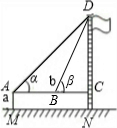
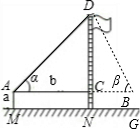
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题---测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
 |
 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: | 解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
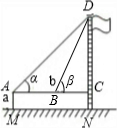
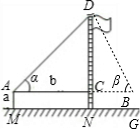
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
 |
 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: |
解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组 活动地点:学校操场
活动时间:××××年××月××日年上午9:00 活动小组组长:×××
数学活动报告
活动小组:第一组 活动地点:学校操场
活动时间:××××年××月××日年上午9:00 活动小组组长:×××
| 课题 | 测量校内旗杆高度 |
| 目的 | 运用所学数学知识及数学方法解决实际问题--测量旗杆高度 |
| 示意图 | 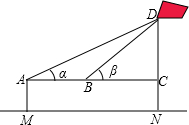 |
| 测量工具 | 皮尺、测角仪 |
| 测量数据: | AM=1.5m,AB=10m,∠α=30°,∠β=60° |
| 计算过程(结 果保留根号) |
解: |
| 测量结果 | DN= |
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 | 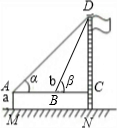 | 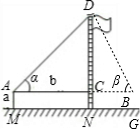 | |
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
| 计算过程(结 果保留根号) | 解: | 解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题---测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 | 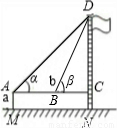 | 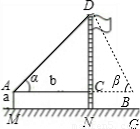 | |
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
| 计算过程(结 果保留根号) | 解: | 解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)