题目内容
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
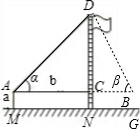
示意图 |  |  | |
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
| 计算过程(结 果保留根号) | 解: | 解: | |
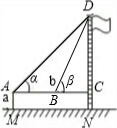
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
解:
方案一(计算过程)
在Rt△ACD中,AC=DC•cotαRt△BCD中,BC=DC•cotβ,
∵AB=AC-BC,∴(cot30°-cot60°)DC=10,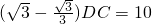 ,
,
解得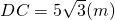 ;
;
∵AM=CN,∴DN=DC+CN=DC+AM=(5 +1.5)m;
+1.5)m;
(测量结果):DN=(5 +1.5)m;
+1.5)m;
方案二(计算过程)
在Rt△ACD中,AC=DC÷tanαRt△BCD中,BC=DC÷tanβ,
∵AB=AC+BC,∴ ,
,
解得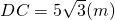
∵AM=CN,∴DN=DC+CN=DC+AM=(5 +1.5)m;
+1.5)m;
(测量结果):DN=(5 +1.5)m;
+1.5)m;
方案三(不惟一)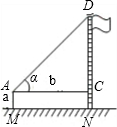
能正确画出示意图
(测量工具):皮尺、测角仪;(测量数据):AM=a,AC=b,∠DAC=α
(计算过程)解:在Rt△ACD中,CD=b•tanα,
∵DN=DC+CN,AM=CN,
∴DN=b•tanα+a;
(测量结果):DN=b•tanα+a.
分析:(1)方案一与方案二均涉及多个直角三角形,应结合图形中直角三角形的角边关系,构造方程关系式,进而可求出答案.
(2)根据题意,设计测量方法,要求符合三角函数的定义,且易于操作即可.
点评:【命题意图】本题是以活动报告的形式呈现,要求学生在阅读理解的基础上,进行有关测量方案的设计.当然,这里所需解决的问题并非阅读方案就能解决的,需要学生观察、分析比较,进行适度的转化与迁移,从而确定新方案.此外,在几何背景中需要学生对几何图形的直观感受,最终需要学生进行清晰的书面表达,因而本题较好地考查了直角三角形的有关知识和阅读理解、几何直觉、合情推理、书面表达等多种能力,较好的体现了对数学活动过程的考查.
方案一(计算过程)
在Rt△ACD中,AC=DC•cotαRt△BCD中,BC=DC•cotβ,
∵AB=AC-BC,∴(cot30°-cot60°)DC=10,
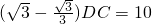 ,
,解得
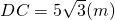 ;
;∵AM=CN,∴DN=DC+CN=DC+AM=(5
 +1.5)m;
+1.5)m;(测量结果):DN=(5
 +1.5)m;
+1.5)m;方案二(计算过程)
在Rt△ACD中,AC=DC÷tanαRt△BCD中,BC=DC÷tanβ,
∵AB=AC+BC,∴
 ,
,解得
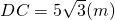
∵AM=CN,∴DN=DC+CN=DC+AM=(5
 +1.5)m;
+1.5)m;(测量结果):DN=(5
 +1.5)m;
+1.5)m;方案三(不惟一)

能正确画出示意图
(测量工具):皮尺、测角仪;(测量数据):AM=a,AC=b,∠DAC=α
(计算过程)解:在Rt△ACD中,CD=b•tanα,
∵DN=DC+CN,AM=CN,
∴DN=b•tanα+a;
(测量结果):DN=b•tanα+a.
分析:(1)方案一与方案二均涉及多个直角三角形,应结合图形中直角三角形的角边关系,构造方程关系式,进而可求出答案.
(2)根据题意,设计测量方法,要求符合三角函数的定义,且易于操作即可.
点评:【命题意图】本题是以活动报告的形式呈现,要求学生在阅读理解的基础上,进行有关测量方案的设计.当然,这里所需解决的问题并非阅读方案就能解决的,需要学生观察、分析比较,进行适度的转化与迁移,从而确定新方案.此外,在几何背景中需要学生对几何图形的直观感受,最终需要学生进行清晰的书面表达,因而本题较好地考查了直角三角形的有关知识和阅读理解、几何直觉、合情推理、书面表达等多种能力,较好的体现了对数学活动过程的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某校九年级(3)班在体育毕业考试中,全班所有学生得分的情况如下表所示:
那么该班共有 人,随机地抽取1人,恰好是获得30分的学生的概率是 ,从上表中,你还能获取的信息是 .(写出一条即可)
| 分数段 | 18分以下 | 18~20分 | 21~23 | 24~26 | 27~29 | 30分 |
| 人数 | 2 | 3 | 12 | 20 | 18 | 10 |
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题---测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
 |
 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: | 解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
数学活动报告
活动小组:第一组
活动地点:学校操场
活动时间:××××年××月××日年上午9:00
活动小组组长:×××
| 课题 | 测量校内旗杆高度 | ||
| 目的 | 运用所学数学知识及数学方法解决实际问题----测量旗杆高度 | ||
| 方案 | 方案一 | 方案二 | 方案三 |
示意图 |
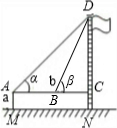 |
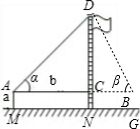 |
|
| 测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
| 测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° |
AM=1.5m,AB=20m ∠α=30°,∠β=60° |
|
| 计算过程(结 果保留根号) |
解: |
解: | |
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组 活动地点:学校操场
活动时间:××××年××月××日年上午9:00 活动小组组长:×××
数学活动报告
活动小组:第一组 活动地点:学校操场
活动时间:××××年××月××日年上午9:00 活动小组组长:×××
| 课题 | 测量校内旗杆高度 |
| 目的 | 运用所学数学知识及数学方法解决实际问题--测量旗杆高度 |
| 示意图 | 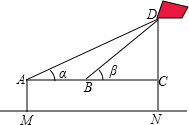 |
| 测量工具 | 皮尺、测角仪 |
| 测量数据: | AM=1.5m,AB=10m,∠α=30°,∠β=60° |
| 计算过程(结 果保留根号) |
解: |
| 测量结果 | DN= |