题目内容
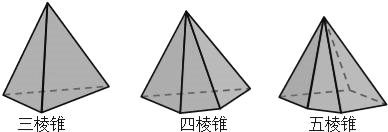
【题目】设棱锥的顶点数为V,面数为F,棱数为E.
(1)观察与发现:三棱锥中,V3= ,F3= ,E3= ;
五棱锥中,V5= ,F5= ,E5= ;
(2)猜想:①十棱锥中,V10= ,F10= ,E10= ;
②n棱锥中,Vn= ,Fn= ,En= ;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系: ;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E= ;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.
【答案】(1)4,4,6;6,6,10;(2)11,11,20;n+1,n+1,2n;(3)V=F,V+F﹣2.(4)V+F﹣E=2.
【解析】
(1)观察与发现:根据三棱锥、五棱锥的特征填写即可;
(2)猜想:①根据十棱锥的特征填写即可;
②根据n棱锥的特征的特征填写即可;
(3)探究:①通过列举得到棱锥的顶点数(V)与面数(F)之间的等量关系;
②通过列举得到棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系;
(4)拓展:根据棱柱的特征得到棱柱的顶点数(V)、面数(F)、棱数(E)之间的等量关系.
解:(1)观察与发现:三棱锥中,V3=4,F3=4,E3=6;
五棱锥中,V5=6,F5=6,E5=10;
(2)猜想:①十棱锥中,V10=11,F10=11,E10=20;
②n棱锥中,Vn=n+1,Fn=n+1,En=2n;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系:V=F;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E=V+F﹣2;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间也存在某种等量关系,相应的等式是:V+F﹣E=2.
故答案为:4,4,6;6,6,10;11,11,20;n+1,n+1,2n;V=F,V+F﹣2.

【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?