题目内容
【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.

【答案】(1)证明见解析;(2)∠BEP+![]() ∠EPF=180.证明见解析;(3)∠EPF=135
∠EPF=180.证明见解析;(3)∠EPF=135
【解析】试题分析:(1)延长FP交AB于点Q,根据平行线性质可得∠2=∠3,再由∠1=∠2可得∠1=∠3,即可证明结论;(2)过点P作PM∥CD,即可证得JK∥AB∥CD∥PM,根据平行线的性质解答即可;(3)作PG∥AB,MH∥AB,则PG∥MH∥AB∥CD,根据平行线的性质进行分析解答即可.
试题解析:
延长EP交CD于点Q
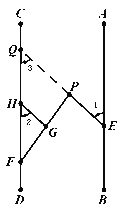
∵GH∥PE,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴AB∥CD.
(2)过点P作PM∥CD,又AB∥CD,∴PM∥AB.

∴∠FPM=∠1,∠EPM=∠2,
∴∠FPE=∠FPM+∠EPM=∠1+∠2.
又∵JK∥AB∥CD,
同理可证:∠FJE=∠CFJ+∠2.
又∵∠FJK=∠CFJ=2∠1=∠3=∠2,
∵∠BEP+∠3=180,
∴∠BEP+2∠1=180,
∴∠BEP+2(∠EPF-∠2)=180,
∴∠BEP+2∠EPF-2∠2=180,
∴∠BEP+2∠EPF-2(180-∠BEP)=180.
即:![]()
(3)作PG∥AB,MH∥AB,则PG∥MH∥AB∥CD.
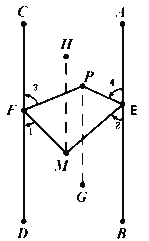
∵FM⊥EM,∴∠EMF=90
易证:∠1+∠2=∠EMF=90,∠EPF=∠3+∠4,
又∵∠3=∠PFM,∠4=∠PEM,
∴∠1=180-2∠3,∠2=180-2∠4.
∴180-2∠3+180-2∠4=90,
∴2∠3+2∠4=270.
∴∠3+∠4=135,
∴∠EPF=135

 教材全解字词句篇系列答案
教材全解字词句篇系列答案