题目内容
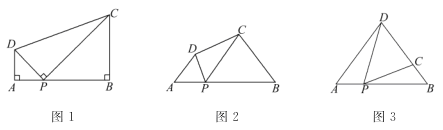
【题目】已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向三角形外作等边△ABD和等边△ACE.
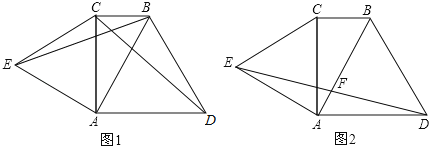
(1)如图1,连接线段BE、CD.求证:BE=CD;
(2)如图2,连接DE交AB于点F.求证:F为DE中点.
【答案】(1)证明见解析(2)证明见解析
【解析】此题考查了全等三角形的判定与性质,平行线的性质,以及等边三角形的性质,
(1)由△ABD和△ACE是等边三角形,根据等边三角形的性质得到AB=AD,AC=AE,∠DAB=∠EAC=60°,然后给∠DAB和∠EAC都加上∠BAC,得到∠DAC=∠BAE,利用“SAS“即可得到△DAC≌△BAE,最后根据全等三角形的对应边相等即可得证;
(2)作DG∥AE,交AB于点G,由等边三角形的∠EAC=60°,加上已知的∠CAB=30°得到∠FAE=90°,然后根据两直线平行内错角相等得到∠DGF=90°,再根据∠ACB=90°,∠CAB=30°,利用三角形的内角和定理得到∠ABC=60°,由等边三角形的性质也得到∠DBG=60°,从而得到两角的相等,再由DB=AB,利用“AAS”证得△DGB≌△ACB,根据全等三角形的对应边相等得到DG=AC,再由△AEC为等边三角形得到AE=AC,等量代换可得DG=AE,加上一对对顶角的相等和一对直角的相等根据“AAS”证得△DGF≌△EAF,最后根据全等三角形的对应边相等即可得证.
(1)∵△ABD和△ACE是等边三角形,
∴AB=AD,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,
在△DAC和△BAE中,

∴△DAC≌△BAE(SAS),
∴DC=BE;
(2)如图,作DG∥AE,交AB于点G,

由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,
∴∠DGF=∠FAE=90°,
又∵∠ACB=90°,∠CAB=30°,
∴∠ABC=60°,
又∵△ABD为等边三角形,∠DBG=60°,DB=AB,
∴∠DBG=∠ABC=60°,
在△DGB和△ACB中,

∴△DGB≌△ACB(AAS),
∴DG=AC,
又∵△AEC为等边三角形,∴AE=AC,
∴DG=AE,
在△DGF和△EAF中,
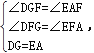
∴△DGF≌△EAF(AAS),
∴DF=EF,即F为DE中点.

【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.