��Ŀ����
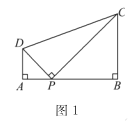
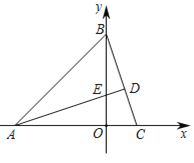
����Ŀ�� (1)�����⣺��ͼ1�����ı���ABCD�У���PΪAB��һ�㣬��DPC=��A=��B=90������֤��AD��BC=AP��BP��
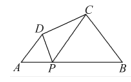
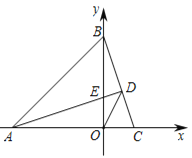
(2)��̽������ͼ2�����ı���ABCD�У���PΪAB��һ�㣬����DPC=��A=��B=��ʱ�����������Ƿ���Ȼ������˵�����ɣ�
(3)��Ӧ�ã������ã�1����2����õľ��������⣺
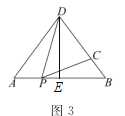
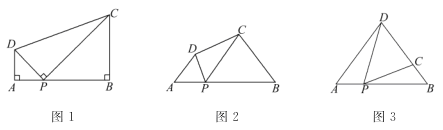
��ͼ3������ABD�У�AB=6��AD=BD=5����P��ÿ��1����λ���ȵ��ٶȣ��ɵ�A �������ر�AB���B�˶�����������DPC=��A�����P���˶�ʱ��Ϊt���룩����DC�ij�����ABD�ױ��ϵĸ����ʱ����t��ֵ��
���𰸡�(1)��֤�����̼�������(2)��֤�����̼�������(3)��t=1���5��.
��������
���������(1)��������DPC=��A=��B=90���ó���ADP+��APD=��BPC+��APD=90��������ADP=��BPC���Ӷ��ó���ADP����BPC���ƣ��Ӷ��ó��𰸣�(2)������ͬ����֤�������ó����������ƣ��Ӷ��ó��𰸣�(3)������D��DE��AB�ڵ�E����AE=BE=3�����ݹ��ɶ����ó�DE=4����AP=t����BP=6��t������(1)(2)�Ķ����г�����t�ķ��̣��Ӷ����t��ֵ.
���������(1)����ͼ1 �ߡ�DPC=��A=��B=90�������ADP+��APD=90����
��BPC+��APD=90�������ADP =��BPC ���ADP�ס�BPC����![]() ��AD��BC=AP��BP��
��AD��BC=AP��BP��
(2)������AD��BC=AP��BP �Գ�����
���ɣ���ͼ2���ߡ�BPD=��DPC+��BPC�� ���ߡ�BPD=��A+��ADP�����DPC+��BPC =��A+��ADP��
�ߡ�DPC =��A=�������BPC =��ADP ���ߡ�A=��B=�������ADP�ס�BPC����![]()
��AD��BC=AP��BP��
(3)����ͼ3������D��DE��AB�ڵ�E����AD=BD=5��AB=6�� ��AE=BE=3���ɹ��ɶ�����DE=4��
��DC=DE=4����BC=5-4=1������AD=BD�����A=��B������֪����DPC =��A�����DPC =��A=��B��
�ɣ�1������2���ɵã�AD��BC=AP��BP�� ��AP=t��BP=6-t����t��6-t��=5��1��
���t1=1��t2=5�� ��t��ֵΪ1���5�룮