题目内容
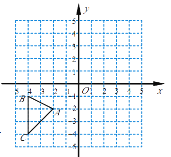
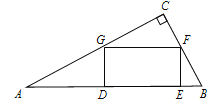
【题目】如图,矩形 ![]() 的顶点
的顶点 ![]() 、
、![]() 、
、![]() 都在坐标轴上,点
都在坐标轴上,点 ![]() 的坐标为
的坐标为 ![]() ,
,![]() 是
是 ![]() 边的中点.
边的中点.
(1)求出点 ![]() 的坐标和
的坐标和 ![]() 的周长;(直接写出结果)
的周长;(直接写出结果)
(2)若点 ![]() 是矩形
是矩形 ![]() 的对称轴
的对称轴 ![]() 上的一点,使以
上的一点,使以 ![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求出符合条件的点
为顶点的四边形是平行四边形,求出符合条件的点 ![]() 的坐标;
的坐标;
(3)若 ![]() 是
是 ![]() 边上一个动点,它以每秒
边上一个动点,它以每秒 ![]() 个单位长度的速度从
个单位长度的速度从 ![]() 点出发,沿
点出发,沿 ![]() 方向向点
方向向点 ![]() 匀速运动,设运动时间为
匀速运动,设运动时间为 ![]() 秒.是否存在某一时刻,使以
秒.是否存在某一时刻,使以 ![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与 ![]() 相似或全等? 若存在,求出此时
相似或全等? 若存在,求出此时 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
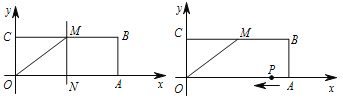
【答案】(1)![]() ,周长为
,周长为![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)根据四边形OABC是矩形和M是BC边的中点,求出点M的坐标,根据勾股定理求出OM的长,得到△COM的周长;
(2)分以OC,OM为边的平行四边形COMQ和以OC,CM为边的平行四边形COQM两种情况讨论即可;
(3)分∠PMO=90和∠MPO=90两种情况,根据相似或全等三角形的性质解答即可.
解:(1)![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() .
.
![]() ,
,![]() 为
为![]() 中点,
中点,
![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
![]() 的周长
的周长![]() .
.
![]() 点
点![]() ,
,![]() 的周长为
的周长为![]() .
.
(2)分情况讨论:
当四边形是以![]() ,
,![]() 为边的平行四边形
为边的平行四边形![]() ,
,
则![]() ,
,![]() .此时
.此时![]() ;
;
当四边形是以![]() ,
,![]() 为边的平行四边形
为边的平行四边形![]() ,
,
则![]() 点是对称轴
点是对称轴![]() 与
与![]() 轴的交点,此时
轴的交点,此时![]() ;
;
综上所述,符合条件的点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
(3)存在.
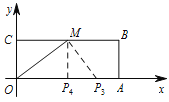
如图.由题意知![]() 不可能等于
不可能等于![]() ,分两种情况:
,分两种情况:
当![]() 时,
时,![]() ,
,
![]() .
. ![]() .
.
![]() .
. ![]() .
.
当![]() 时,
时,![]() ,
,
![]() .
.
![]() .
.
![]() .
.
综上所述,当为![]() 或
或![]() 时,
时,![]() 与
与![]() 相似或全等.
相似或全等.
故答案为:(1)![]() ,周长为
,周长为![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.

 愉快的寒假南京出版社系列答案
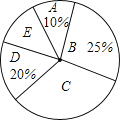
愉快的寒假南京出版社系列答案【题目】近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.
组别 | A | B | C | D | E |
时间t(分钟) | t<40 | 40≤t<60 | 60≤t<80 | 80≤t<100 | t≥100 |
人数 | 12 | 30 | a | 24 | 12 |
(1)求出本次被调查的学生数;
(2)请求出统计表中a的值;
(3)求各组人数的众数;
(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.