Question

【题目】如图1，用篱笆靠墙围成矩形花围ABCD，墙可利用的最大长度为15米，一面利用旧墙，其余三面用篱笆围成，篱笆总长为24米．

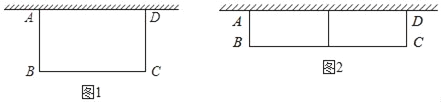
(1)若围成的花圃面积为40米2时，求BC的长；

(2)如图2若计划在花圃中间用一道隔成两个小矩形，且围成的花圃面积为50米2，请你判断能否成功围成花圃，如果能，求BC的长？如果不能，请说明理由．

Answer 1

【答案】(1) BC的长为4米；(2) 不能围成，理由见解析.

【解析】

(1）由于篱笆总长为24m，设平行于墙的BC边长为x m，由此得到，接着根据题意列出方程，解方程即可求出BC的长；
（2）不能围成花圃；设BC的长为y米，则AB的长为米,，此方程的判别式△=（-24）2-4×150＜0，由此得到方程无实数解，所以不能围成花圃；

(1)设BC的长度为x米，则AB的长度为米，

根据题意得：x=40，

整理得：x2﹣24x+80=0，

解得：x1=4，x2=20．

∵20＞15，

∴x2=20舍去．

答：BC的长为4米．

(2)不能围成，理由如下：

设BC的长为y米，则AB的长为米，

根据题意得：y =50，

整理得：y2﹣24y+150=0．

∵△=（﹣24）2﹣4×1×150=﹣24＜0，

∴该方程无实数根，

∴不能围成面积为50米2的花圃．