��Ŀ����
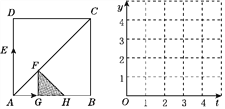
����Ŀ����ͼ��ֱ��l��y=![]() x+m��x�ύ��A�㣬�Ҿ�����B����
x+m��x�ύ��A�㣬�Ҿ�����B����![]() ��2������֪������C��y=ax2+bx+9��x��ֻ��һ�������㣬ǡΪA�㣮
��2������֪������C��y=ax2+bx+9��x��ֻ��һ�������㣬ǡΪA�㣮
��1����m��ֵ����BAO�Ķ�����
��2����������C�ĺ�������ʽ��
��3����������C��x������ƽ�ƣ���ƽ�ƺ��������ΪC1���䶥��ΪP��
ƽ�ƺ���PAB��ֱ��AB���۵õ���DAB����D�ܷ�����������C1�ϣ�
���ܣ������ʱ����P�����ꣻ�粻�ܣ�˵�����ɣ�

���𰸡���1��m=3����BAO=30������2��y=![]() ��x+3
��x+3![]() ��2����3���ܣ�P������Ϊ��21
��2����3���ܣ�P������Ϊ��21![]() ��0����
��0����
��������
�����������1����B���������ֱ��l�Ľ���ʽ�������m��ֵ�����ֱ��l�Ľ���ʽ����ֱ��l��y�ύ�ڵ�C�����C�����������������Ǻ������������BAO�Ķ�������2��������֪�������߱ض�����0��9������������x��ֻ��һ��������A����A���������ߵĶ��㣬���Կ����������ߵĶ���ʽy=a��x+3![]() ��2������0��9�����붥��ʽ�������a��ֵ����3����P������Ϊ��h��0����������֪����P������A����࣬���Ե�P��A���Ҳ࣬���ڵ�P��D����AB�Գƣ��ҵ�D��������������C1�ϣ��������D���������������C1�Ľ���ʽ�������h��ֵ��
��2������0��9�����붥��ʽ�������a��ֵ����3����P������Ϊ��h��0����������֪����P������A����࣬���Ե�P��A���Ҳ࣬���ڵ�P��D����AB�Գƣ��ҵ�D��������������C1�ϣ��������D���������������C1�Ľ���ʽ�������h��ֵ��
�����������1����B����![]() ��2������y=
��2������y=![]() x+m����2=��1+m����m=3����ֱ��l�Ľ���ʽΪy=
x+m����2=��1+m����m=3����ֱ��l�Ľ���ʽΪy=![]() x+3����ֱ��l��y�ύ�ڵ�C,��x=0����y=
x+3����ֱ��l��y�ύ�ڵ�C,��x=0����y=![]() x+3����y=3����C������Ϊ��0��3������y=0����y=
x+3����y=3����C��������0��3������y=0����y=![]() x+3����x=��3
x+3����x=��3![]() ����A����������3
����A����������3![]() ��0������OC=3��OA=3
��0������OC=3��OA=3![]() ����tan��BAO=
����tan��BAO=![]() =
=![]() �����BAO=30������2����x=0����y=ax2+bx+9����y=9,��������C������0��9��������������C��x��ֻ��һ�������㣬ǡΪA�㣬��A����������C�Ķ��㣬�������ߵĶ���ʽΪy=a��x+3
�����BAO=30������2����x=0����y=ax2+bx+9����y=9,��������C������0��9��������������C��x��ֻ��һ�������㣬ǡΪA�㣬��A����������C�Ķ��㣬�������ߵĶ���ʽΪy=a��x+3![]() ��2���ѣ�0��9������y=a��x+3
��2���ѣ�0��9������y=a��x+3![]() ��2����a=
��2����a=![]() ����������C�Ľ���ʽΪy=
����������C�Ľ���ʽΪy=![]() ��x+3
��x+3![]() ��2����3����������C1�Ľ���ʽΪy=
��2����3����������C1�Ľ���ʽΪy=![]() ��x��h��2������P��A�����ʱ����Dһ������������C1�ϣ���������������⣬����P��A���Ҳ�ʱ����ʱ��P��h��0����AP=h+3
��x��h��2������P��A�����ʱ����Dһ������������C1�ϣ���������������⣬����P��A���Ҳ�ʱ����ʱ��P��h��0����AP=h+3![]() ���ɶԳ��Կ�֪��AD=AP=h+3
���ɶԳ��Կ�֪��AD=AP=h+3![]() ����DAB=��PAB=30��������D��DE��x���ڵ�E����AE=
����DAB=��PAB=30��������D��DE��x���ڵ�E����AE=![]() AD=
AD=![]() ��DE=
��DE=![]() AE=
AE=![]() ����D��������
����D��������![]() ��
��![]() ������D��
������D��![]() ��
��![]() ������y=
������y=![]() ��x��h��2����
��x��h��2����![]() =
=![]() ��
��![]() ��2����h=21
��2����h=21![]() ��h=��3
��h=��3![]() ����h=��3
����h=��3![]() ʱ����ʱP��A�غϣ�������������⣬����������P������Ϊ��21
ʱ����ʱP��A�غϣ�������������⣬����������P������Ϊ��21![]() ��0����
��0����