题目内容
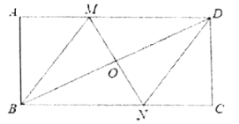
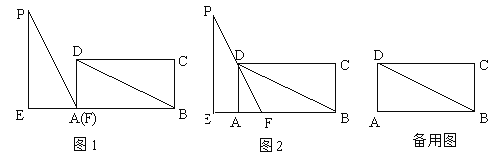
【题目】如图1,在矩形ABCD中,DB=6,AD=3,在Rt△PEF中,∠PEF=90°,EF=3,PF=6,△PEF(点F和点A重合)的边EF和矩形的边AB在同一直线上.现将Rt△PEF从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,
解答下列问题:
(1)如图1,连接PD,填空:∠PFD= ,四边形PEAD的面积是 ;
(2)如图2,当PF经过点D时,求 △PEF运动时间t的值;
(3)在运动的过程中,设△PEF与△ABD重叠部分面积为S,请求出S与t的函数关系式.
【答案】(1)300,![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】(1)根据锐角三角形函数可求出角的度数,然后根据勾股定理求出PE的长,再根据梯形的面积公式求解.
(2)当PF经过点D时,PE∥DA,由EF=3,PF=6,可得∠EPD=∠ADF=30°,用三角函数计算可得AF=t=![]() ;
;
(3)根据题意,分三种情况:①当0≤t<![]() 时,②
时,②![]() ≤t<3时,③3≤t≤6时,根据三角形、梯形的面积的求法,求出S与t的函数关系式即可.
≤t<3时,③3≤t≤6时,根据三角形、梯形的面积的求法,求出S与t的函数关系式即可.
(1)∵在Rt△PEF中,∠PEF=90°,EF=3,PF=6
∴sin∠P=![]()
∴∠P=30°
∵PE∥AD
∴∠PAD=300,
根据勾股定理可得PE=3![]() ,
,
所以S四边形PEAD=![]() ×(3
×(3![]() +3)×3=
+3)×3=![]() ;
;
(2)当PF经过点D时,PE∥DA,由EF=3,PF=6,得∠EPF=∠ADF=30°,
在Rt△ADF中,由AD=3,得AF=![]() ,所以t=
,所以t=![]() ;
;
(3)分三种情况讨论:
①当0≤t<![]() 时, PF交AD于Q,∵AF=t,AQ=
时, PF交AD于Q,∵AF=t,AQ=![]() t,∴S=
t,∴S=![]() ×t×
×t×![]() t=
t=![]() ;
;
②当![]() ≤t<3时,PF交BD于K,作KH⊥AB于H,∵AF=t,∴BF=3
≤t<3时,PF交BD于K,作KH⊥AB于H,∵AF=t,∴BF=3![]() -t,S△ABD=
-t,S△ABD=![]() ,
,
∵∠FBK=∠FKB,∴FB=FK=3![]() -t,KH=KF×sin600=
-t,KH=KF×sin600=![]() ,∴S=S△ABD﹣S△FBK =
,∴S=S△ABD﹣S△FBK =![]()
③当3≤t≤3![]() 时,PE与BD交O,PF交BD于K,∵AF=t,∴AE=t-3,BF=3
时,PE与BD交O,PF交BD于K,∵AF=t,∴AE=t-3,BF=3![]() -t,
-t,
BE=3![]() -t+3,OE=BE×tan300=
-t+3,OE=BE×tan300=![]() ,∴S=
,∴S=![]() 。
。

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案