Question

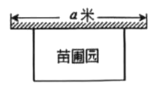
【题目】光明农场准备修建一个矩形苗圃园，苗圃一边靠墙，其他三边用长为48米的篱笆围成.已知墙长为米.设苗圃园垂直于墙的一边长为米.

（1）求当为多少米时，苗圃园面积为280平方米；

（2）若=22米，当取何值时，苗圃园的面积最大，并求最大面积.

Answer 1

【答案】（1）10米或14米;（2）当x=13米时，苗圃园的最大值为286平方米.

【解析】

（1）根据题意可以找出面积与的关系式，代入求值即可；

（2）根据题意和a的值，可以求得x的取值范围，然后根据（1）中的函数关系式即可解答本题.

（1）解：设面积为y,

由题意可得，
解：（1）由题意可得，
y=x（48-2x）=-2x2+48x，
即y与x的函数关系式是y=-2x2+48x，

当y=280时，

280=-2x2+30x

解得x=10或14

所以当为10米或14米时，苗圃园的面积为280平方米

（2）∵a=22，
∴0＜48-2x≤22，
解得，13≤x＜24，
∵y=-2x2+48x=-2（x-12）2+288

当x=13米时，y=-2×（13-12）2+288=286平方米

综上所述，当x=13米时，苗圃园的最大值为286平方米.