题目内容
【题目】如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD,过点D作DH⊥AB于H. 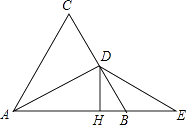
(1)求∠BAD和∠BDE的度数;
(2)求证:点H是AE的中点.
【答案】
(1)解:∵在等边△ABC,且D是AC的中点,
∴∠DAB= ![]() ∠BAC=
∠BAC= ![]() ×60°=30°,∠ABC=60°,
×60°=30°,∠ABC=60°,
∵BE=BD,
∴∠BDE=∠E,
∵∠ABC=∠BDE+∠E,
∴∠BDE=∠E=30°,
∴∠BAD=30°,∠BDE=30°
(2)证明:由(1)可知,∠DAB=∠E=30°
∴AD=ED,△ADE为等腰三角形,
又∵DH⊥AE,
∴H是AE的中点.
【解析】(1)根据等腰三角形的三线合一,可得∠DAB=30°,根据∠ABC=60°,BD=BE,推出∠E=30°.(2)要证M是BE的中点,根据题意可知,证明△BDE△为等腰三角形,利用等腰三角形的高和中线向重合即可得证.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目