��Ŀ����
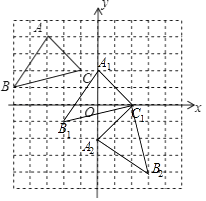
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳����ǵ�λ1����ABC���������㶼�ڸ���ϣ����������ƽ��ֱ������ϵ����������⣺
��1������ABC����ƽ��3����λ����������ƽ��2����λ���ȣ���������ƽ�ƺ�ġ�A1B1C1��
��2��д��A1��C1�����ꣻ
��3������A1B1C1��C1��ʱ����ת90�㣬������ת��ġ�A2B2C1 �� ���A1B1C1��ת������ɨ�����������������У�
���𰸡�
��1���⣺��ͼ����A1B1C1Ϊ����
��2���⣺A1��0��2����C1��2��0��
��3���⣺��ͼ����A2B2C1Ϊ������

S��A1B1C=4��3�� ![]() ��4��1��
��4��1�� ![]() ��2��2��
��2��2�� ![]() ��2��3=5��
��2��3=5��
B1C1= ![]() =
= ![]() ��
��
���ԡ�A1B1C1��ת������ɨ�������=S��A1B1C1+S����B1C1B2
= ![]() +5
+5
= ![]() ��+5
��+5
����������1������2�����õ�ƽ�Ƶ�����������ÿ��������ͬ��ƽ�ƣ�д��A��B��C�Ķ�Ӧ��A1��B1��C1�����꣬Ȼ�����õ���A1B1C1���ɣ���3������������ص����ת�����ʣ�д����A1��B1�Ķ�Ӧ��A2��B2�����꣬�����õ���A2B2C1������������ĺͲ�����![]() ��Ȼ��������ε������ʽ�����á�A1B1C1��ת������ɨ�������=
��Ȼ��������ε������ʽ�����á�A1B1C1��ת������ɨ�������=![]() +S����B1C1B2���м��㼴����������
+S����B1C1B2���м��㼴����������
�����㾫�������ڱ��⿼�������������㹫ʽ����Ҫ�˽���Բ�ϣ��������뾶��һ�λ�Χ�ɵ�ͼ�ν������Σ��������S=�У�R2-r2�����ܵó���ȷ�𰸣�

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��Ϊ����֧�ֶ����д��������������й�����ij�̼Ҽƻ��ӳ��Ҳɹ�A��B��������Ʒ��20������Ʒ�IJɹ����ۣ�Ԫ/�����Dzɹ������������������Ϣ���±���ʾ��
�ɹ����������� | 2 | 4 | 6 | �� |
A��Ʒ���ۣ�Ԫ�� | 1460 | 1420 | 1380 | �� |
B��Ʒ���ۣ�Ԫ�� | 1280 | 1260 | 1240 | �� |
��1����B��Ʒ�IJɹ�����Ϊx���������ɹ�����Ϊy1��Ԫ/��������y1��x�Ĺ�ϵʽ��
��2�����̼��볧��Э�̣��ɹ�A��Ʒ������������B��Ʒ������ ![]() ����B��Ʒ�ɹ����۲�����1250Ԫ������̼ҹ��м��ֽ���������
����B��Ʒ�ɹ����۲�����1250Ԫ������̼ҹ��м��ֽ���������
��3�����̼ҷֱ���1760Ԫ/����1700Ԫ/�������۵����۳�A��B���ֲ�Ʒ����ȫ�����꣬�ڣ�2���������£���ɹ�A�ֲ�Ʒ���ټ�ʱ������������������