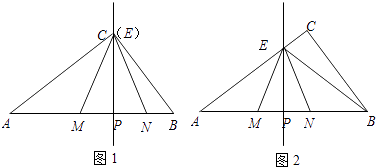题目内容
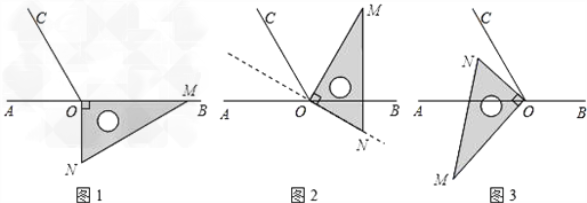
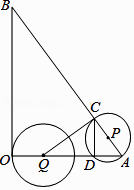
【题目】如图，在Rt△ACB中，∠ACB=90°，∠A=30°，点D是AB边的中点．
（1）如图1，若CD=4，求△ACB的周长．
（2）如图2，若E为AC的中点，将线段CE以C为旋转中心顺时针旋转60°，使点E至点F处，连接BF交CD于点M，连接DF，取DF的中点N，连接MN，求证：MN=2CM．
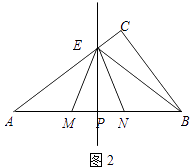
（3）如图3，以C为旋转中心将线段CD顺时针旋转90°，使点D至点E处，连接BE交CD于M，连接DE，取DE的中点N，连接交MN，试猜想BD、MN、MC之间的关系，直接写出其关系式，不证明．
【答案】（1）12+4
；（2）证明见解析；（3）证明见解析.
【解析】（1）根据直角三角形斜边中线的性质，直角三角形30度角性质以及勾股定理即可解决问题．
（2）如图2中，作BQ⊥CD于Q，FP∥MN交DC的延长线于P．首先证明△BQM≌△FCM，推出QC=2CM，再证明△BQC≌△FCP，推出PF=BC=2QC，再根据三角形中位线定理即可解决问题．
（3）结论：（
BD）2+（BD-CM）2=MN2．作BQ⊥CD于Q，连接QN，只要证明△QMN是直角三角形，QN=BD，QM=BD-CM即可解决问题．
如图1中，
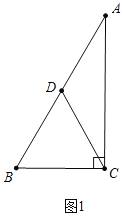
在Rt△ACB中，∵∠ACB=90°，∠A=30°，点D是AB边的中点．
∴CD=BD=AD=4，BC=AB=4，
∴AC=
=
，
∴△ABC的周长为4+8+4=12+4．
（2）证明：如图2中，作BQ⊥CD于Q，FP∥MN交DC的延长线于P．
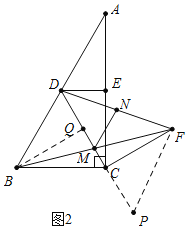
∵△BDC是等边三角形，边长为2，
∴高BQ=2，∠DCB=60°，∠ACD=30°
∵EA=EC=2，
∴CE=CF=BQ，
∵∠ECF=60°，∠ACD=30°，
∴∠DCF=90°，
∴∠BQM=∠MCF=90°，
在△BQM和△FCM中，
，
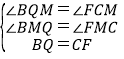∴△BQM≌△FCM，
∴QM=MC．QC=2MC，
∵DN=NF，MN∥FP，
∴DM=MP，
∴DQ=CP=QC，
在△BQC和△FCP中，
，
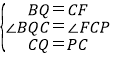∴△BQC≌△FCP，
∴PF=BC=DC=2QC，
∵MN=PF，
∴MN=QC=2CM．
（3）解：如图3中，结论：（BD）2+（BD-CM）2=MN2．理由如下：
作BQ⊥CD于Q，连接QN，
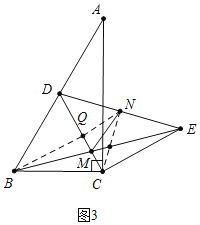
∵△BDC是等边三角形，
∴∠DBQ=30°，
∴DQ=QC=BD，
∵DC=CE，DC⊥CE，
∴∠CDE=∠CED=45°，
∵DQ=QC，DN=NE，
∴QN∥EC，
∴∠QDN=∠NQM=∠DCE=90°，
∴∠QDN=∠QND=45°，
∴QD=QN=BD，
∵QN2+QM2=MN2，
∴（BD）2+（BD-CM）2=MN2．
