题目内容
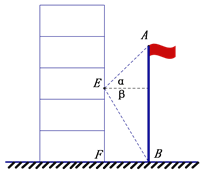
【题目】如图，扶梯AB的坡比(BE与AE长度之比)为4：3，滑梯CD的坡比(CF与DF长度之比)为1：2，设AE=30米，BC=30米，一男孩从扶梯走到滑梯的顶部，然后从滑梯滑下，他共经过了多少路程(即AB+BC+CD的长度)？(结果保留根号)
【答案】他共经过了（80＋
）米
【解析】
根据坡比和已知条件即可求出BE、CF和DF，再根据勾股定理即可求出AB和CD，从而得出结论．
解：∵扶梯AB的坡比为4：3，即BE：AE=4：3，滑梯CD的坡比为1：2，即CF：DF=1：2，AE=30米，BC=30米，
∴BE=
=40米，CF=BE=40米，DF=2CF=80米
根据勾股定理可得：AB=
米，CD=
米
∴AB＋BC＋CD=（80＋）米
答：他共经过了（80＋）米．
练习册系列答案
相关题目
