题目内容
【题目】如果一个三角形能用一条直线将其分割出两个等腰三角形,那么我们称这个三角形为“活三角形”,这条直线称为该“活三角形”的“生命线”.
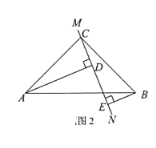
(1)小明在研究“活三角形”问题时(如图),他发现,在△ABC中,若∠BAC = 3∠C时,这个△ABC一定是“活三角形”.点D在BC边上一点,联结AD,他猜测:当∠DAC = ∠C时,AD就是这个三角形的“生命线”,请你帮他说明AD是△ABC的“生命线”的理由.

(2)如小明研究结果可以总结为:有一个内角是另一个内角的3倍时,该三角形是一个“活三角形”.
请通过自己操作研究,并根据上诉结论,总结“活三角形”的其他特征.
(注意从三角形边、角特征及相互间关系总结)
,该三角形是一个“活三角形”.
,该三角形是一个“活三角形”.
(3)如果一个等腰三角形是一个“活三角形”那么它的顶角大小为: 度.(直接写出结果即可)
【答案】(1)详见解析;(2)有一个内角是另一个内角2倍时;有一个内角为直角时;(3)90°,108°,36°,![]()
【解析】
(1)证明△ADC和△ABD为等腰三角形即可;
(2)作∠CAD=∠C,则∠ADB=2∠C,当∠ABD=2∠C时,∠ABD=∠ADB,则△ABC为“活三角形”;由直角三角形斜边的中线等于斜边的一半,易证直角三角形为“活三角形”;
(3)分四种情况讨论,根据三角形内角和为180°建立方程,解方程求出顶角即可.
解:(1)∵∠DAC =∠C,
∴∠ADB=2∠C,△ADC为等腰三角形,
又∵∠BAC=3∠C,
∴∠BAD=2∠C=∠ADB,
∴△ABD为等腰三角形,
∴AD是△ABC的“生命线”;
(2)∠ADB=2∠C,当∠ABD=2∠C时,∠ABD=∠ADB,则△ABC为“活三角形”,
即:有一个内角是另一个内角的2倍时,该三角形是一个“活三角形”;
当∠BAC=90°,AD为斜边BC的中线,则△ABC为“活三角形”,
即:有一个内角为直角时,该三角形是一个“活三角形”,
故答案为:有一个内角是另一个内角的2倍时;有一个内角为直角时
(3)①由(2)可知,直角三角形为“活三角形”,故等腰直角三角形也为“活三角形”,即顶角为90°;
②如图,△ABC为等腰三角形,AB=AC,
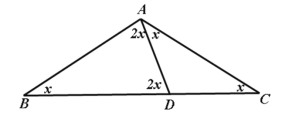
则有![]() ,
,
解得:![]() ,
,
顶角∠BAC=108°;
③如图,△ABC为等腰三角形,AB=AC,
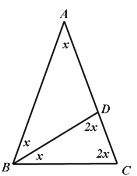
则有,![]() 。,
。,
解得:![]() ,
,
顶角∠BAC=36°;
④如图,△ABC为等腰三角形,AB=AC,
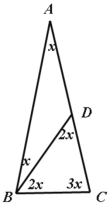
则![]() ,
,
解得:![]() ,
,
即顶角∠BAC=![]() ,
,
综上:顶角为90°,108°,36°,![]() .
.