Question

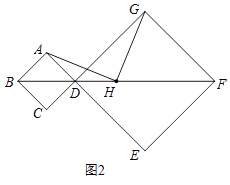
【题目】为了发展乡村旅游，洪江村准备在洪江河道上修一座与河道垂直的吊桥，如图1所示，直线l、m代表洪江河的两岸，且l∥m，点A是洪江村自助农场的所在地，点B是洪江村游乐园所在地．

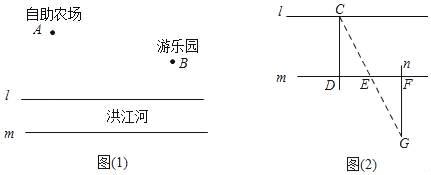
问题1：吊桥的选址

吊桥准备选在到A、B两地的距离之和刚好为最小的点C处，即在直线l上找到使（AC+BC）的值为最小的点C的位置．请利用你所学的知识帮助村委会设计选址方案（直接在图1里作图），并简单说明你所设计方案的原理

问题2：河道的宽度

在测量河道的宽度时，施工队在河道南侧的开阔地用以下方法（如图2所示）：①作CD⊥1，与河对岸的直线m相交于D；②在直线m上取E、F两点，使得DE＝EF＝10米；③过点F作m的垂线n；④在直线n上找到一点G，使得点G与C、E两点在同一直线上；⑤测量FG的长度为20米．请问你知道河道的宽度吗？说明理由

Answer 1

【答案】问题1：吊桥的选址，理由：两点之间线段最短，问题2：河道的宽度为20米

【解析】

问题1：作点A关于直线l的对称点A′，连接BA′交直线l于C，连接AC，此时AC+BC的值最小．

问题2：：只要证明△CDE≌△GFE，可得CD＝GF；

问题1：吊桥的选址．

如图，作点A关于直线l的对称点A′，连接BA′交直线l于C，连接AC，此时AC+BC的值最小．

理由：两点之间线段最短．

问题2：如图2中，

在Rt△CDE和Rt△GFE中，

，

∴△CDE≌△GFE，

∴CD＝FG＝20米，

答：河道的宽度为20米．