题目内容
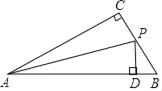
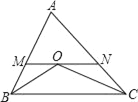
【题目】如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB相交于点O,线段MN过点O与AB、AC分别交于M、N两点,且MN∥BC,若△AMN的周长等于12,则AB+AC的长等于_____.
【答案】12
【解析】
根据BO平分∠CBA,CO平分∠ACB,且MN∥BC,可得出MO=MB,NO=NC,所以三角形AMN的周长是AB+AC.
解:∵BO平分∠CBA,CO平分∠ACB,
∴∠MBO=∠OBC,∠OCN=∠OCB,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠OCB,
∴∠MBO=∠MOB,∠NOC=∠NCO,
∴MO=MB,NO=NC,
∵△AMN的周长等于12,
∴△AMN的周长=AM+MN+AN=AB+AC=12.
故答案为:12.

练习册系列答案
相关题目