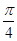题目内容
在边长为a的正方形内有4个等圆，每相邻两个互相外切，它们中每一个至少与正方形的一边相切，那么此等圆的半径可能是（ ）
A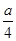． | B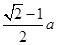． | C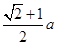． | D． |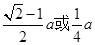
D
此题要考虑两种情况：
当四个等圆两两外切且和每个圆和正方形的两边相切时，
则圆的直径的2倍等于正方形的边长，
即圆的半径是；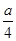
当只有每相邻的两个圆相外切且和正方形的一边相切时，
则它们的圆心组成了一个边长等于圆的直径的正方形．
若设圆的半径是r，则有2r+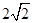
r=a，
r=．
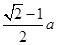故选D．
当四个等圆两两外切且和每个圆和正方形的两边相切时，
则圆的直径的2倍等于正方形的边长，
即圆的半径是
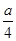；当只有每相邻的两个圆相外切且和正方形的一边相切时，
则它们的圆心组成了一个边长等于圆的直径的正方形．
若设圆的半径是r，则有2r+
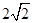r=a，r=
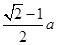．故选D．
练习册系列答案
相关题目
