题目内容
【题目】如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,求∠BOE的度数. 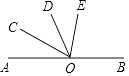
【答案】解:设∠DOE=x,则∠BOE=2x, ∵∠BOD=∠BOE+∠EOD
∴∠BOD=3x
∴∠AOD=180°﹣∠BOD=180°﹣3x
∵OC平分∠AOD
∴∠COD= ![]() ∠AOD=90°﹣
∠AOD=90°﹣ ![]() x
x
∵∠COE=∠COD+∠DOE=90°﹣ ![]() x+x=90°﹣
x+x=90°﹣ ![]()
∴90°﹣ ![]() =α
=α
∴x=180°﹣2α,即∠DOE=180°﹣2α
∴∠BOE=360°﹣4α
【解析】设∠DOE=x,则∠BOE=2x,用含x求出∠COE的表达式,然后根据∠COE=α列出方程即可求出∠BOE的度数.
【考点精析】利用角的平分线和角的运算对题目进行判断即可得到答案,需要熟知从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.

练习册系列答案
相关题目