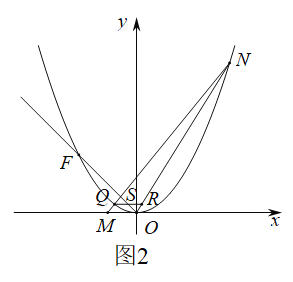
题目内容
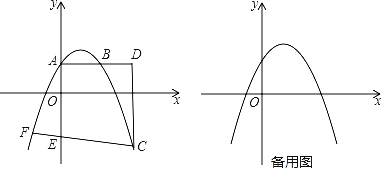
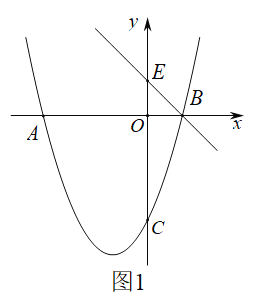
【题目】如图是二次函数y＝ax2+bx+c的图象，其对称轴为直线x＝1，且与x轴的一个交点为A(3，0)，下列说法错误的是（ ）
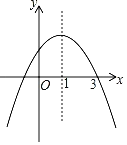
A.b2＞4acB.abc＜0
C.4a﹣2b+c＞0D.当x＜﹣1时，y随x的增大而增大
【答案】C
【解析】
由抛物线的开口方向和与x轴的交点个数可得a＜0，c＞0，b＝﹣2a＞0，∴△＝b2﹣4ac＞0，可判断选项A，B，由抛物线的对称性可得抛物线与x轴的另一个交点为（﹣1，0），可得当x＜﹣1时，y随x的增大而增大，当x＝﹣2时，y＜0，即4a﹣2b+c＜0，可判断C，D选项，即可求解．
解：∵抛物线开口向下，顶点在第一象限，
∴抛物线与x轴有两个交点，a＜0，c＞0，
∴△＝b2﹣4ac＞0，
∴b2＞4ac，所以A选项不合题意；
∵抛物线的对称轴为直线x＝1，
∴﹣
＝1，即b＝﹣2a＞0，
∴abc＜0，所以选项B不合题意；
∵对称轴为直线x＝1，且与x轴的一个交点为A（3，0），
∴抛物线与x轴的另一个交点为（﹣1，0）
∴当x＜﹣1时，y随x的增大而增大，
当x＝﹣2时，y＜0，即4a﹣2b+c＜0，
故选项C符合题意，选项D不符合题意，
故选：C．
【题目】在新冠疫情防控期间，某医疗器械商业集团新进了40台A型电子体温测量仪，60台B型电子体温测量仪，计划调配给下属的甲、乙两个连锁店销售，其中70台给甲连锁店，30台给乙连锁店．两个连锁店销售这两种测量仪每台的利润(元)如下表：
A型 | B型 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店
台A型测量仪，集团卖出这100台测量仪的总利润为
(元)．
（1）求关于的函数关系式，并求出的取值范围：
（2）为了促销，集团决定仅对甲连锁店的A型测量仪每台让利
元销售，其他的销售利润不变，并且让利后每台A型测量仪的利润仍然高于甲连锁店销售的每台B型测量仪的利润，问该集团应该如何设计调配方案，使总利润达到最大?
