题目内容
在Rt△ABC中,CB=4,CA=3,AB=5,点P为三条角平分线的交点,则点P到各边的距离都是 .
1
解:如图,连接OB,
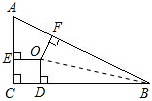
∵点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,
∴OE=OF=OD,
又∵OB是公共边,
∴Rt△BOF≌Rt△BOD(Hz),
∴BD=BF,
同理,AE=AF,CE=CD,
∵∠C=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE,
∴OECD是正方形,
设OE=OF=OD=x,则CE=CD=x,BD=BF=4-x,AF=AE=3-x,
∴BF+FA=AB=5,即4-x+3-x=5,
解得x=1.
则OE=OF=OD=1,即点P到各边的距离都是1.

∵点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,
∴OE=OF=OD,
又∵OB是公共边,
∴Rt△BOF≌Rt△BOD(Hz),
∴BD=BF,
同理,AE=AF,CE=CD,
∵∠C=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE,
∴OECD是正方形,
设OE=OF=OD=x,则CE=CD=x,BD=BF=4-x,AF=AE=3-x,
∴BF+FA=AB=5,即4-x+3-x=5,
解得x=1.
则OE=OF=OD=1,即点P到各边的距离都是1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

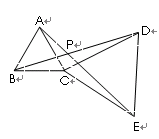


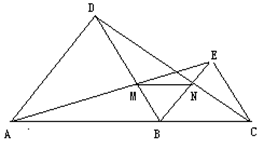

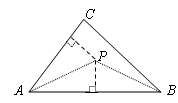
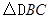 中,
中,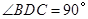 ,
, 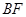 平分
平分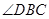 ,与
,与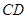 相交于点
相交于点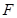 ,延长
,延长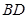 到
到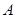 ,使
,使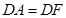 ,延长
,延长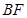 交
交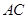 于
于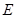 ,
,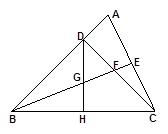
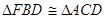 ;
;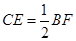 ;
;