题目内容
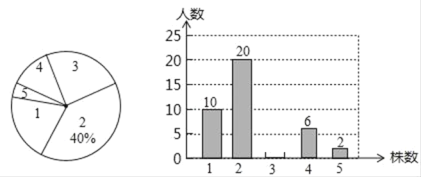
【题目】为选拔参加八年级数学“拓展性课程”活动人选，数学李老师对本班甲、乙两名学生以前经历的10次测验成绩（分）进行了整理、分析（见图①）：
学生 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 83.7 | a | 86 | 13.21 |
乙 | 83.7 | 82 | b | 46.21 |
（1）写出a，b的值；
（2）如要推选1名学生参加，你推荐谁？请说明你推荐的理由．
【答案】（1）84.5；81；（2）甲或乙.
【解析】
（1）依据中位数和众数的定义进行求解即可；
（2）依据平均数、中位数、方差以及众数的角度分析，即可得到哪个学生的水平较高．
（1）甲组数据排序后，最中间的两个数据为：84和85，故中位数a=
×（84+85）=84.5，
乙组数据中出现次数最多的数据为81，故众数b=81；
（2）甲，理由：两人的平均数相同且甲的方差小于乙，说明甲成绩稳定；
或：乙，理由：在90≤x≤100的分数段中，乙的次数大于甲．（答案不唯一，理由须支撑推断结论）．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
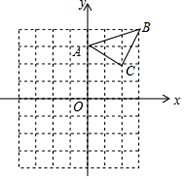
【题目】已知△A′B′C′是由△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如下表所示：
△ABC | A（a，0） | B（3，0） | C（5，5） |
△A′B′C′ | A′（4，2） | B′（7，b） | C′（c，7） |
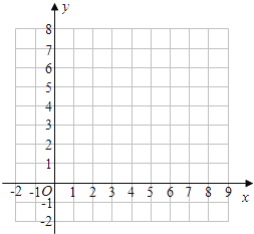
（1）观察表中各对应点坐标的变化，并填空：a=________，b=________，c=________；
（2）在平面直角坐标系中画出△ABC及平移后的△A′B′C′；
（3）直接写出△A′B′C′的面积是________．
