��Ŀ����
����Ŀ����ͼ1��ֱ��![]() �ֱ���x�ᡢy�ύ��A��B���㣬��ֱ��
�ֱ���x�ᡢy�ύ��A��B���㣬��ֱ��![]() ���ڵ�
���ڵ�![]() ��ƽ����y���ֱ��l��ԭ��O��������ÿ��1����λ���ȵ��ٶ���x������ƽ�ƣ���C��ʱֹͣ��ֱ��l�ֱ��߶�BC��OC��x���ڵ�D��E��P����DEΪб�������������ֱ��
��ƽ����y���ֱ��l��ԭ��O��������ÿ��1����λ���ȵ��ٶ���x������ƽ�ƣ���C��ʱֹͣ��ֱ��l�ֱ��߶�BC��OC��x���ڵ�D��E��P����DEΪб�������������ֱ��![]() ����ֱ��l���˶�ʱ��Ϊt(��)��
����ֱ��l���˶�ʱ��Ϊt(��)��
(1)��գ�k=____��b=____��
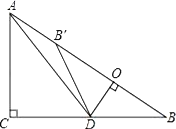
(2)��tΪ��ֵʱ����F��y����(��ͼ2��ʾ)��
(3)��![]() ��
��![]() �ص����ֵ����ΪS����ֱ��д��S��t�ĺ�����ϵʽ(��Ҫ��д������)����д��t��ȡֵ��Χ��
�ص����ֵ����ΪS����ֱ��д��S��t�ĺ�����ϵʽ(��Ҫ��д������)����д��t��ȡֵ��Χ��

���𰸡�(1)![]() ��4��(2)t=1��(3)S=��t��2��2��
��4��(2)t=1��(3)S=��t��2��2��
��������
��1�����ô���ϵ�����������k��b��ֵ��
��2����F��y����ʱ��F��DE�ľ������DE�ij���һ�����ݴ˼����з������t��ֵ��
��3����F��y��������Ҳ��������������������F��y������ʱ����Ӱ��������������ֱ������������IJ�����F��y����Ҳ�ʱ����Ӱ���־��ǡ�DEF����������������ε������ʽ������ú����Ľ���ʽ��
��1���ѣ�2��![]() ������y=��
������y=��![]() x+b������
x+b������![]() +b=
+b=![]() �������b=4��
�������b=4��
�ѣ�2��![]() ������y=kx����2k=
������y=kx����2k=![]() �������k=
�������k=![]() ��
��
�ʴ�Ϊ��![]() ��4��
��4��
��2���ɣ�1������ֱ�ߵĽ���ʽΪ��
y=��![]() x+4��y=
x+4��y=![]() x�����������OP=t����D��t����
x�����������OP=t����D��t����![]() t+4����E��t��
t+4����E��t��![]() t����
t����
��DE=��2t+4����FG��DE��G����FG=OP=t��
�ߡ�DEF�ǵ���ֱ����������FG��DE����FG=![]() DE����t=
DE����t=![]() ����2t+4���������t=1��
����2t+4���������t=1��
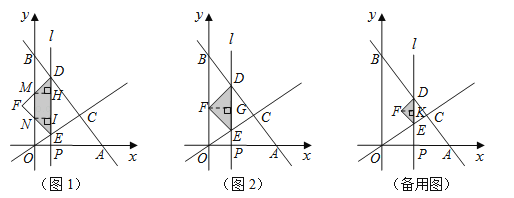
��3����0��t��1ʱ����ͼ1����S��DEF=![]() ����
����![]() t+4��
t+4��![]() t��
t��![]() ����
����![]() t+4��
t+4��![]() t��=
t��=![]() ����2t+4��2=��t��2��2����y�����߲����ǵ���ֱ�����������ױ��ϵĸ�����
����2t+4��2=��t��2��2����y�����߲����ǵ���ֱ�����������ױ��ϵĸ�����![]() ����
����![]() t+4��
t+4��![]() t����t=
t����t=![]() ����2t+4����t=2��2t�������������2��2t��2��
����2t+4����t=2��2t�������������2��2t��2��
S=��t��2��2����2��2t��2=��3t2+4t��
��1��t��2ʱ������ͼ������FK��DE�ڵ�K����
S=��t��2��2��
������������0��t��1ʱ��S=��3t2+4t����1��t��2ʱ��S=��t��2��2��