题目内容
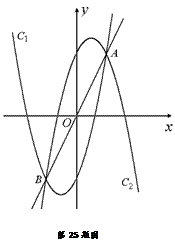
如图,设抛物线C1: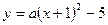 , C2:
, C2: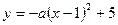 ,C1与C2的交点为A,
,C1与C2的交点为A,
B,点A的坐标是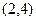 ,点B的横坐标是-2.
,点B的横坐标是-2.
(1)求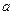 的值及点B的坐标;
的值及点B的坐标;
(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 过C2顶点M的直线记为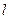 ,且
,且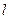 与x轴交于点N.
与x轴交于点N.
①若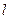 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
②若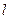 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.
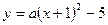 , C2:
, C2: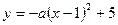 ,C1与C2的交点为A,
,C1与C2的交点为A,B,点A的坐标是
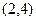 ,点B的横坐标是-2.
,点B的横坐标是-2.(1)求
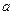 的值及点B的坐标;
的值及点B的坐标; (2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 过C2顶点M的直线记为
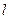 ,且
,且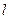 与x轴交于点N.
与x轴交于点N.①若
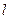 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;②若
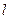 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.
解:(1 )∵点A
)∵点A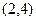 在抛物线C1上,
在抛物线C1上,
∴把点A坐标代入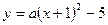 得
得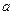 ="1" ……………………………………(2分)
="1" ……………………………………(2分)
∴抛物线C1的解析式为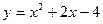
设B(-2,b), ∴ b=-4, ∴ B(-2,-4) …………………………(3分)
(2)①如图1:
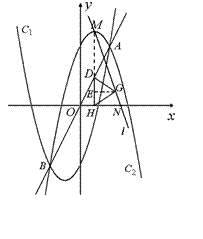
∵ M(1, 5),D(1, 2), 且DH⊥x轴,∴点M在DH上,MH="5."
过点G作GE⊥DH,垂足为E ,
,
由△DHG是正三角形,可得EG= , EH=1,
, EH=1,
∴ ME=4. ………………………………(4分)
设N ( x, 0 ), 则 NH=x-1,
由△MEG∽△MHN,得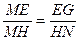 ,
,
∴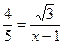 , ∴
, ∴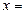
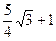 …………(5分))
…………(5分))
∴点N的横坐标为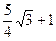 .
.
②当点D 移到与点A重合时,如图2,
移到与点A重合时,如图2,
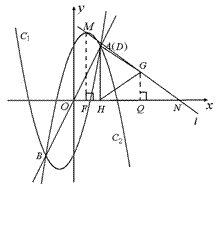
直线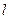 与
与 DG交于点G,此时点N的横坐标最大.
DG交于点G,此时点N的横坐标最大.
过点G,M作x轴的垂线,垂足分别为点Q,F,
设N (x,0)
(x,0)
∵ A (2, 4) ∴ G (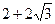 , 2)
, 2)
∴ NQ=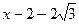 NF =
NF =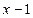 GQ="2 " MF =5.
GQ="2 " MF =5.
∵△NGQ∽△NMF
∴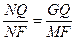
∴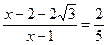
∴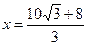 . ………………………………………………………(7分)
. ………………………………………………………(7分)
当点D移到与点B重合时,如图3
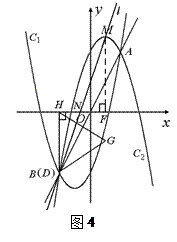
直线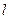 与DG交于点D,即点B
与DG交于点D,即点B
此时点N的横坐标最小.
∵ B(-2, -4) ∴ H(-2, 0), D(-2, -4)
设N(x,0)
∵△BHN∽△MFN,∴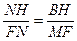
∴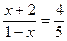 ∴
∴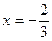

∴点N横坐标的范围为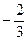 ≤x≤
≤x≤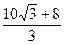 ………………………………(8分)
………………………………(8分)
 )∵点A
)∵点A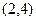 在抛物线C1上,
在抛物线C1上,∴把点A坐标代入
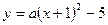 得
得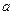 ="1" ……………………………………(2分)
="1" ……………………………………(2分)∴抛物线C1的解析式为
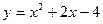
设B(-2,b), ∴ b=-4, ∴ B(-2,-4) …………………………(3分)
(2)①如图1:

∵ M(1, 5),D(1, 2), 且DH⊥x轴,∴点M在DH上,MH="5."
过点G作GE⊥DH,垂足为E
 ,
,由△DHG是正三角形,可得EG=
 , EH=1,
, EH=1,∴ ME=4. ………………………………(4分)
设N ( x, 0 ), 则 NH=x-1,
由△MEG∽△MHN,得
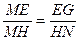 ,
,∴
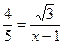 , ∴
, ∴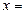
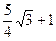 …………(5分))
…………(5分))∴点N的横坐标为
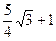 .
. ②当点D
 移到与点A重合时,如图2,
移到与点A重合时,如图2,
直线
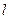 与
与 DG交于点G,此时点N的横坐标最大.
DG交于点G,此时点N的横坐标最大.过点G,M作x轴的垂线,垂足分别为点Q,F,
设N
 (x,0)
(x,0)∵ A (2, 4) ∴ G (
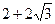 , 2)
, 2)∴ NQ=
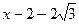 NF =
NF =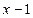 GQ="2 " MF =5.
GQ="2 " MF =5.∵△NGQ∽△NMF
∴
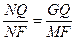
∴
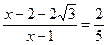
∴
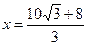 . ………………………………………………………(7分)
. ………………………………………………………(7分) 当点D移到与点B重合时,如图3

直线
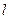 与DG交于点D,即点B
与DG交于点D,即点B此时点N的横坐标最小.
∵ B(-2, -4) ∴ H(-2, 0), D(-2, -4)
设N(x,0)
∵△BHN∽△MFN,∴
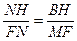
∴
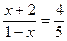 ∴
∴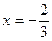

∴点N横坐标的范围为
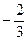 ≤x≤
≤x≤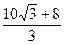 ………………………………(8分)
………………………………(8分)略

练习册系列答案
相关题目
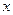 轴相交于点F,点Q为直线AD上一点,且△ABQ与△ADF相似,直接写出点Q点的坐标.
轴相交于点F,点Q为直线AD上一点,且△ABQ与△ADF相似,直接写出点Q点的坐标.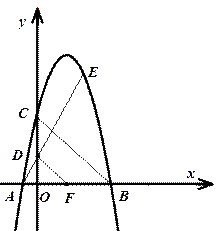

 ,且
,且 ,则b= .
,则b= .  中,
中, ∥
∥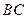 ,且
,且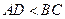 ,
, ,
,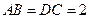 。
。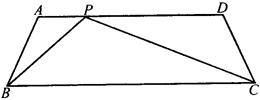
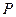 为
为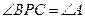 ,求
,求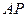 的长;
的长;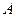 、
、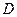 不重合),且满足
不重合),且满足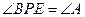 ,
,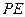 交直线
交直线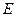 ,同时交直线
,同时交直线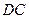 于点
于点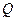 。
。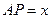 ,
,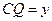 ,求
,求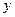 关于
关于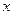 的函数关系式,并写出自变量
的函数关系式,并写出自变量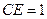 时,写出
时,写出 灯罩底
灯罩底 面半径MK的长;
面半径MK的长;
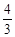 )
) (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F.
